Учням групи 212
Записуємо в робочий зошит тему
Логарифми та їх властивості.
конспект
1. Логарифм числа
| |||||||
Означення
|
Приклади
| ||||||
Логарифмом додатного числа b (b > 0) за основою а (а >0, a ≠1) називається показник с, до якого треба піднести а, щоб одержати b.
Позначення: loga b; loga b=с, ас =b
Дія знаходження логарифма – логарифмування.
|
| ||||||
Десятковий логарифм – це логарифм за основою 10.
Позначення: log10b = lg b
|
lg 1000 = 3, оскільки
103 = 1000
| ||||||
Натуральний логарифм – це логарифм за основою е (е ≈ 2,7182818).
Позначення: logеb = ln b
|
ln
| ||||||
2. Основна логарифмічна тотожність
| |||||||
1)
| |||||||
3. Властивості логарифмів і формули логарифмування
| |||||||
1) loga 1 = 0, а > 0, a ≠ 1
|
Логарифм одиниці за будь-якою основою дорівнює нулю.
|
log7 1 = 0, 70 = 1
| |||||
2) loga а = 1, а > 0, a ≠ 1
|
Логарифм будь-якого числа за такою ж основою дорівнює одиниці.
|
log8 8 = 1, 81 = 8
| |||||
(а > 0, a ≠ 1, x > 0, y > 0)
|
Логарифм добутку додатних чисел дорівнює сумі логарифмів множників.
|
log3 2 + log3 4,5 = log3 (2·4,5)=
= log39 = 2, 32 = 9
| |||||
4)
(а > 0, a ≠ 1, x > 0, y > 0)
|
Логарифм частки при діленні додатних чисел дорівнює різниці логарифмів діленого і дільника.
| ||||||
5)
(а > 0, a ≠ 1, x > 0)
|
Логарифм степені додатного числа дорівнює добутку показника степеню на логарифм основи.
| ||||||
4. Формула переходу до іншої основи
| |||||||
1)
| |||||||
Наслідки
| |||||||
(а > 0, a ≠ 1, b > 0, b ≠ 1)
|
(а > 0, a ≠ 1, b > 0)
|
(а > 0, a ≠ 1, b > 0)
|
(а > 0, a ≠ 1)
| ||||
Переглянути відео за посиланням
1. https://www.youtube.com/watch?v=UQH6YFlzyXE
Самостійна робота
Установіть відповідність між прикладами 1-9 та їхніми розв’язками
1. log2256 = о)1/2
3. log16128 + log162 = ф) 0
4. lg 0,001 = л) 8
5. log42 + log4128 = а)-3
6. log3729 = м) 1
7. log2591 = г) 2
8. log26532653 = и) 6
9. log6432 – log62 = в) 3
Учням групи 212
Записуємо в робочий зошит тему
"Логарифмічна функція та її властивості".
Показникова функція у = аx, а > 0, а ≠ 1
| |
0 < а < 1
| |
1. D(y) = R
3. Зростає
4. Якщо х = 0, то у = 1
5. Якщо х < 0, то у < 1
6. Якщо х > 0, то у > 1
|
2. E(y) = (0; +∞
4. Якщо х = 0, то у = 1
5. Якщо х < 0, то у > 1
|
Переглянути відео за посиланням
Конспект
Функція виду у = logax, де а — задане число, а > 0, а ≠ 1 називається логарифмічною функцією.
Source: https://formula.kr.ua/logarifmichna-funktsiya/logarifmichna-funktsiya-jiji-vlastivosti-ta-grafik.html
Логарифмічна функція має такі властивості:
1) Область визначення функції — множина всіх додатних чисел. Ця властивість випливає із означення логарифма, оскільки вираз logaх має зміст тільки при х > 0.
2) Область значень логарифмічної функції — множина R усіх дійсних чисел. Ця властивість випливає з того, що для будь-якого дійсного числа b є таке додатне число х, що logax = b, тобто рівняння logax = b має єдиний корінь. Такий корінь існує і дорівнює х = аb, оскільки loga аb = b.
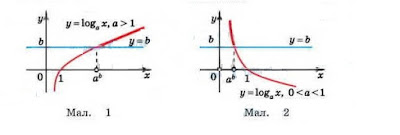
3) Логарифмічна функція на всій області визначення зростає (при а > 1) або спадає (при 0 < а < 1).
Якщо а > 1, то функція у = logax приймає додатні значення при х > 1, від'ємні — при 0 < х < 1.
Якщо 0 < а < 1, то функція у = logax приймає додатні значення при 0 < х < 1, від'ємні — при х > 1.
Побудуємо графіки двох функцій.
Приклад 1
1. y=log2x , основа 2>1
| | | | | | | |
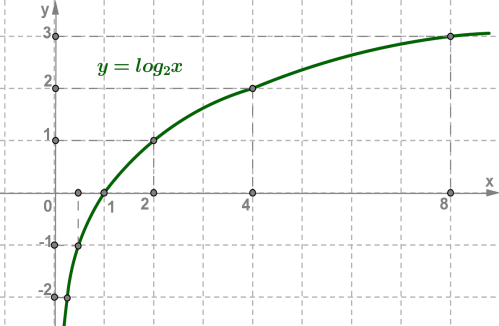
Приклад 2
2. y=log13x основа 0< 13 <1
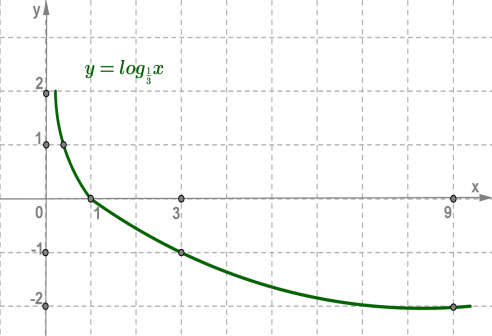
Домашнє завдання
Учням групи 212.
Записуємо в робочий зошит тему
"Логарифмічні рівняння "
Переглянути відео за посиланням
Логарифмічними називають рівняння, які містять змінну під
знаком логарифма.
Розв’язати логарифмічне рівняння – це означає знайти всі його
корені або довести, що рівняння коренів не має.
корені або довести, що рівняння коренів не має.
Приклади розв’язування логарифмічних рівнянь за означенням логарифма.
1. log 2(x-3) = 4;
x - 3 = 24;
x – 3 = 16;
x =19.
2, log 3 (4x + 7) = 2;
4x + 7 =32;
4x + 7 = 9;
4x = 2;
x = 2 : 4;
x = 0,5.
Приклади розв’язування логарифмічних рівнянь за методом потенціювання.
log 3 (4x - 5) = log 3 (7 + 3x);
4x – 5 = 7 + 3x;
4x – 3x = 7 + 5;
x = 12;
Перевірка:
log 3 (4 · 12 - 5) = log 3 (7 + 3 ·12);
log 3 43 = log 3 43.
Відповідь: х = 12.
Приклади розв’язування логарифмічних рівнянь за методом
потенціювання з використанням властивостей логарифма.
lg (x - 9) + lg2 = lg (x + 5);
lg (2 · (x - 9)) = lg (x + 5);
2x – 18 = x + 5;
2x – x = 5 + 18;
x = 23.
ОДЗ :
x – 9 > 0; x > 9;
x + 5 > 0; x > - 5; ОДЗ: х > 9.
Відповідь: х = 23.
Розв’язати самостійно:
1. log 2 (7x - 10) = 5;
2. log x+1 (x2 + 6x - 15) = 2;
3. log 3 (6x + 15) = log 3 (9x - 2);
4. log 2 (x + 2) = log 2 3 + log 2 (x - 6).
Учням групи 212
Записуємо в робочий зошит
Алгоритм розв’язування логарифмічних нерівностей
1. Звести праву і ліву частини нерівності до логарифмів з
однаковими основами.
однаковими основами.
2. Порівняти основу логарифма з 1 і з’ясувати зростаючою чи
спадною є функція.
спадною є функція.
2.1 Якщо функція зростаюча а > 1, то при переході від
логарифмічної нерівності до нерівності, яка не містить логарифмів ,
знак нерівності не змінюємо.
2.2 Якщо функція спадна 0 < а < 1, то при переході від
логарифмічної нерівності до нерівності, яка не містить логарифмів ,
знак нерівності змінюємо на протилежний.
3. Скласти нерівності для ОДЗ (всі під логарифмічні вирази повинні
бути більшими за нуль, а основа логарифма більша за нуль і
не дорівнює 1).
4. Розв’язати утворену систему нерівностей.
не дорівнює 1).
4. Розв’язати утворену систему нерівностей.
Переглянути відео за посиланням
Урок: систематизація знань, розв’язування вправ, підготовкв до контрольної роботи з теми: "Показникова і логарифмічна функції".
Виконуємо тренувальні вправи:
Завдання 1
Завдання 2
Домашнє завдання
Повторити навчальний матеріал по темі "Показникова і логарифмічна функції", підготуватися до тематичної контрольної роботи.
Учням групи 212
Тематична контрольна робота
з теми "Показникова і логарифмічна функції"
Учням групи 212
Записуємо в робочий зошит тему
Записати в зошитах конспект
« Багатогранники. Опуклі багатогранники».
Переглянути ві део за посиланням
Фігури, які вивчає стереометрія, називаються тілами. Наочно тіло уявляють як частину простору, зайняту фізичним тілом і обмежену поверхнею.
Багатогранником називають тіло (частина простору), обмежене скінченою кількістю плоских многокутників.
Багатокутники, які обмежують багатогранник, називають його гранями, їх сторони – ребрами, а вершини – вершинами багатогранника.
Багатогранник називається опуклим, якщо він лежить по один бік від площини кожного з плоских багатокутників на його поверхні.
Прикладами опуклих багатогранників можуть бути куб, прямокутний паралелепіпед, тетраедр тощо.
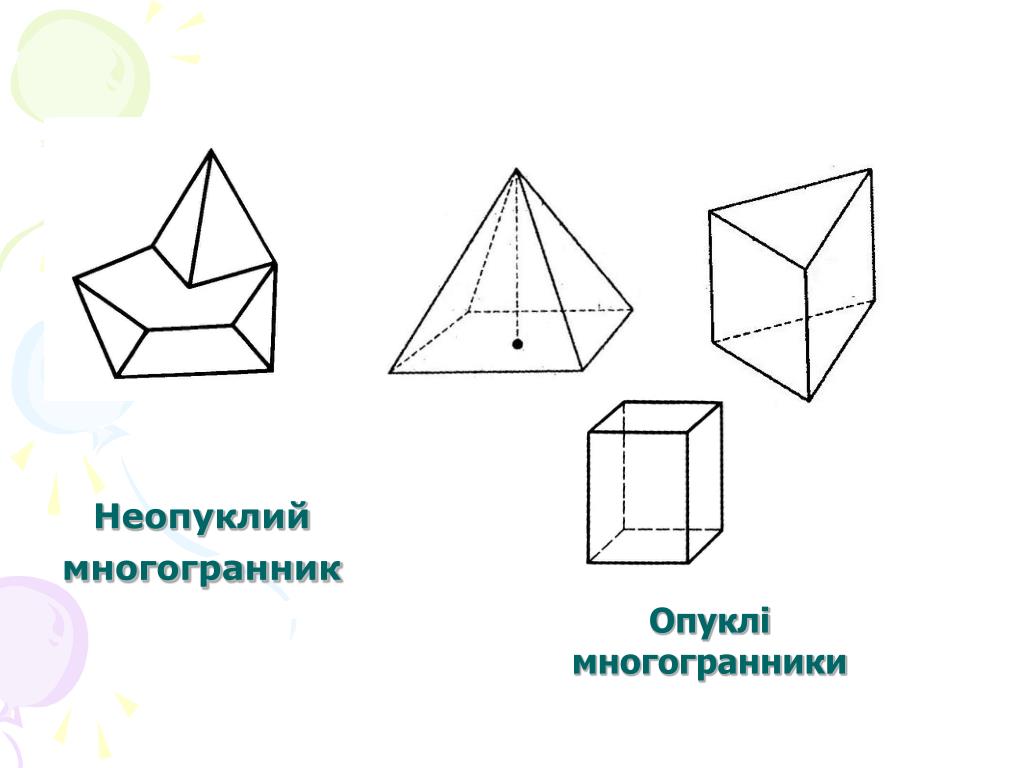
Дайте відповіді на питання:
1. Наведіть приклади предметів побуту, що є геометричними тілами.
3. Наведіть приклади предметів побуту, які мають форму багатогранника.
4. Наведіть приклади речовин, вивчених у курсі хімії, кристали яких мають форму багатогранника.
5. Скільки вершин, ребер, граней має: а) тетраедр; б) куб?
6. Яке найменше число ребер може мати багатогранник?
7. Побудуйте багатогранник, який має 4 грані.
Скільки ребер і скільки вершин він має?
8. Скільки ребер може сходитися у вершині багатогранника?
9. Побудуйте багатогранник, у якого число вершин і число граней однакові.
10.Побудуйте багатогранник, який має 5 граней і 6 вершин. Скільки ребер він має?
Учням групи 212
Записуємо в робочий зошит тему
« Призма. Пряма і правильна призма. Паралелепіпед. Прямокутний паралелепіпед».
Конспект.
1. Призма. Пряма і правильна призма.
Призмою - називається багатогранник, у якого дві грані — рівні n-кутники, розташовані в паралельних площинах, а решта n граней — паралелограми.
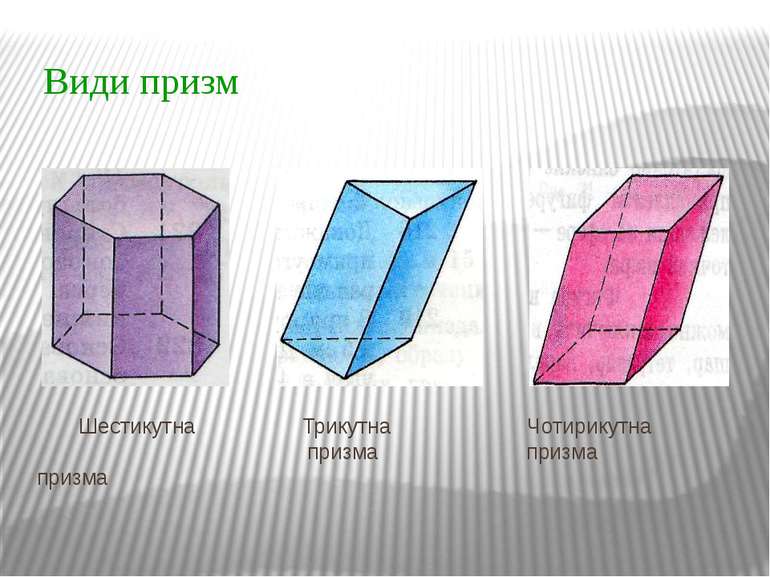
Властивості призми
• Основи призми є рівними багатокутниками.
• Бічні грані призми є паралелограмами.
• Бічні ребра призми рівні.
Висота призми — відстань між площинами її основ.
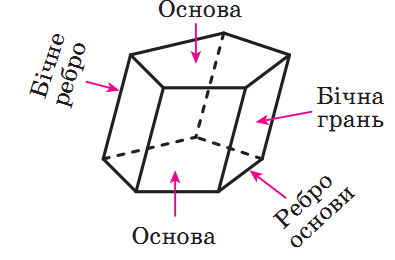
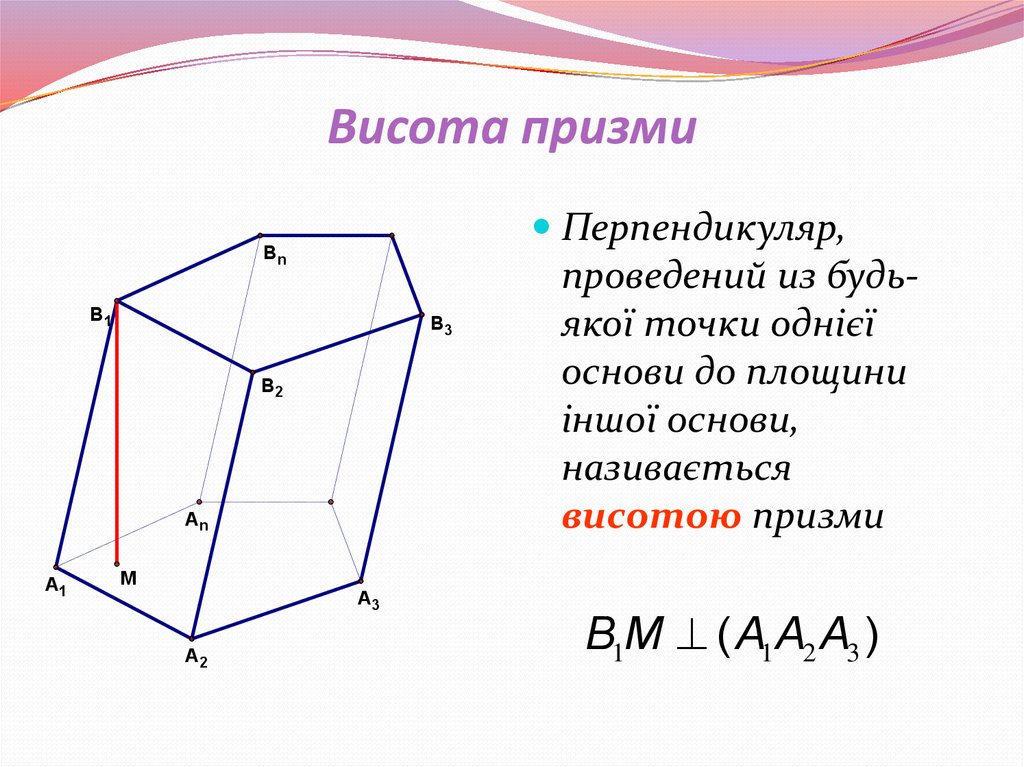
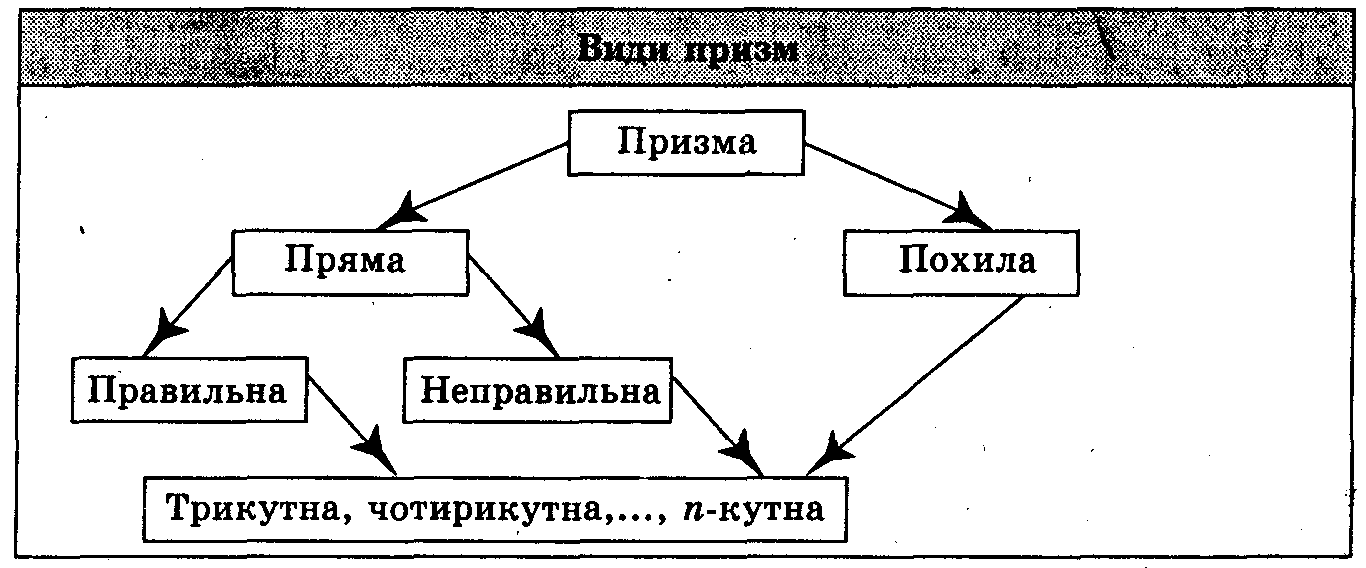
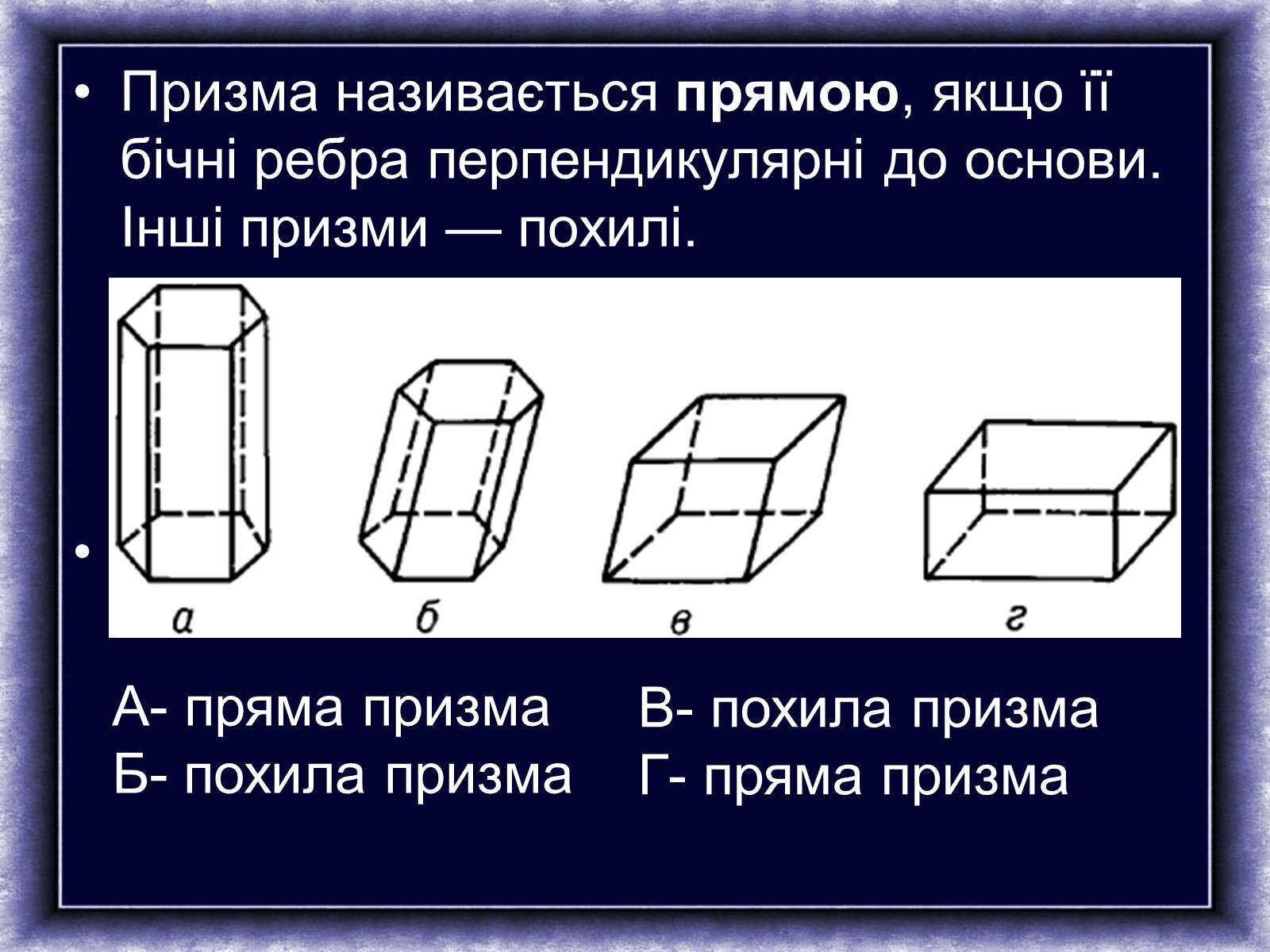
Пряма призма – це призма, що має перпендикулярні до основ бічні ребра. Якщо ця умова не виконується, то призма називається похилою.
У прямої призми всі бічні грані – прямокутники.
Пряма призма, в основі якої лежить правильний багатокутник,
називається правильною призмою.
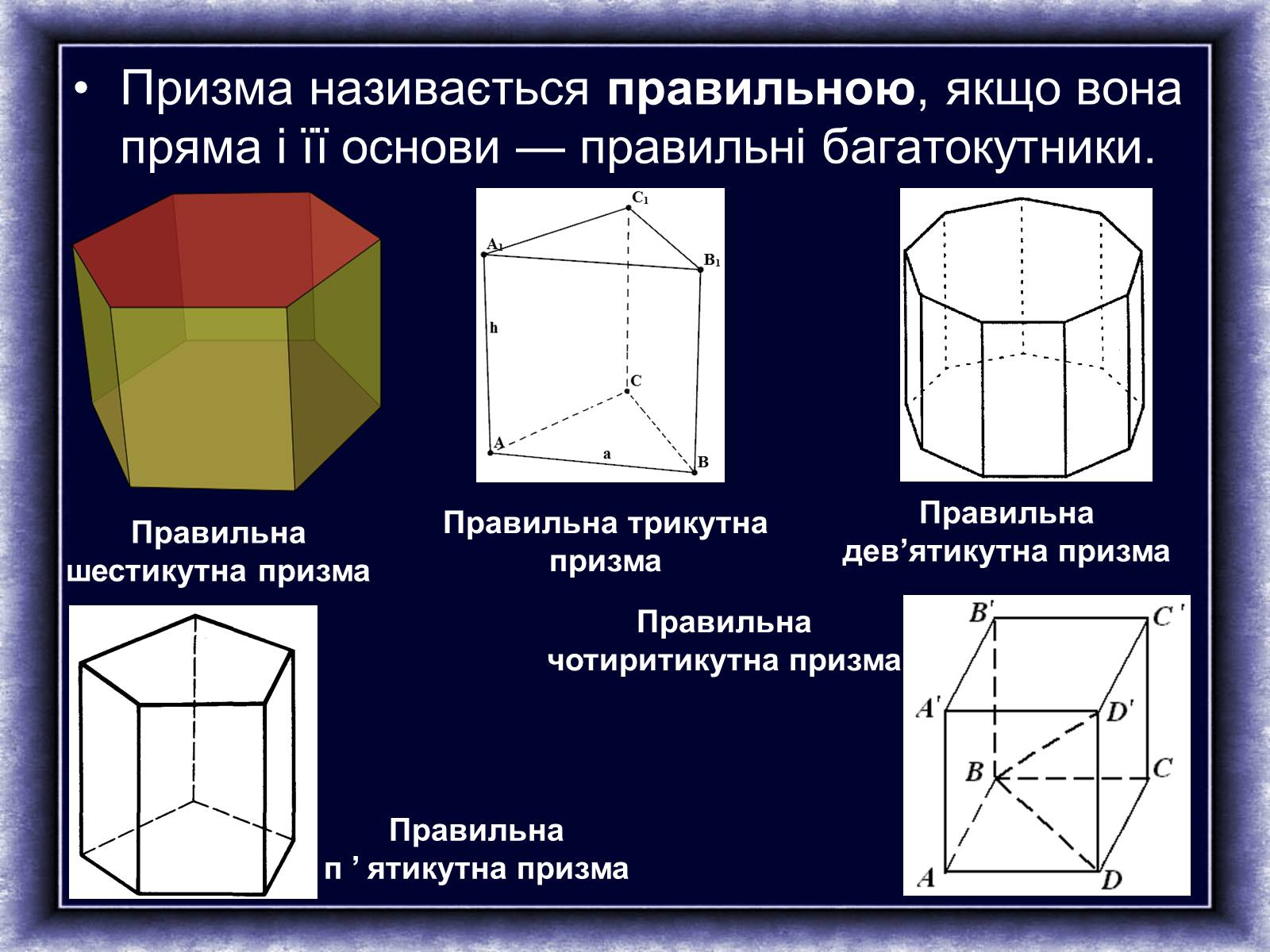
2. Паралелепіпед. Прямокутний паралелепіпед.
Паралелепіпед — це призма, основою якої є паралелограм.
Протилежні грані паралелепіпеда паралельні і рівні.
Діагоналі паралелепіпеда перетинаються в одній точці і діляться нею навпіл
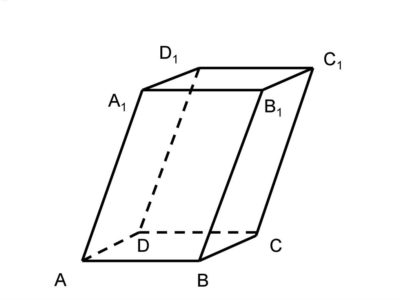
Прямий паралелепіпед - це паралелепіпед, що має перпендикулярні до основ бічні ребра.
Прямокутний паралелепіпед — прямий паралелепіпед , основою якого є прямокутник.
Бічні грані прямокутного паралелепіпеда перпендикулярні його основам.
Лінійними розмірами прямокутного паралелепіпеда є довжини його непаралельних ребер. Прямокутний паралелепіпед, усі лінійні розміри якого рівні, називається кубом.
Прямокутний паралелепіпед — прямий паралелепіпед , основою якого є прямокутник.
Бічні грані прямокутного паралелепіпеда перпендикулярні його основам.
Лінійними розмірами прямокутного паралелепіпеда є довжини його непаралельних ребер. Прямокутний паралелепіпед, усі лінійні розміри якого рівні, називається кубом.
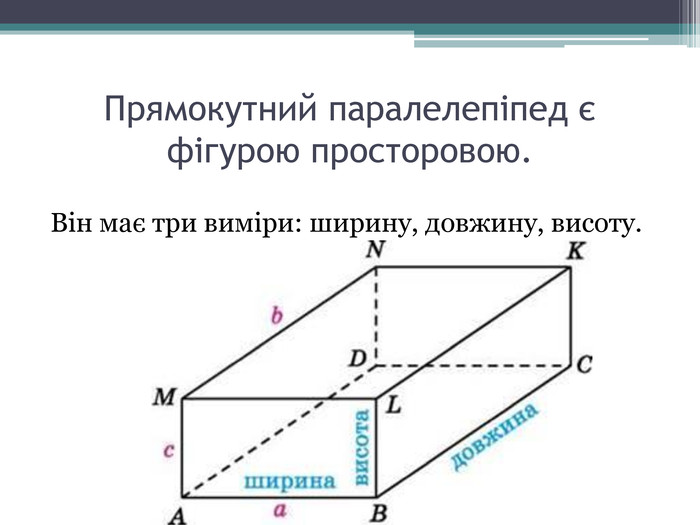
Діагоналі прямокутного паралелепіпеда рівні.
Усі двогранні кути прямокутного паралелепіпеда – прямі.
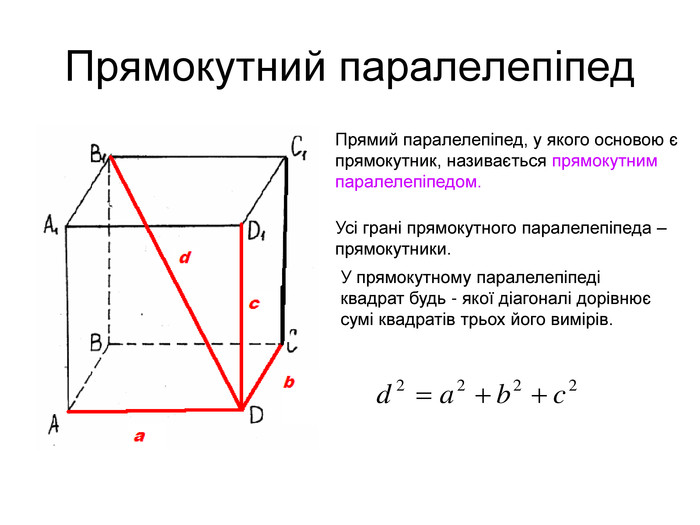
Квадрат будь-якої діагоналі прямокутного паралелепіпеда є сумою квадратів трьох його вимірів.
Точка перетину діагоналей паралелепіпеда є його центром симетрії.
Через центр симетрії прямокутного паралелепіпеда проходять три площини, паралельні граням, які є площинами симетрії прямокутного паралелепіпеда.
Усі двогранні кути прямокутного паралелепіпеда – прямі.
Квадрат будь-якої діагоналі прямокутного паралелепіпеда є сумою квадратів трьох його вимірів.
Точка перетину діагоналей паралелепіпеда є його центром симетрії.
Через центр симетрії прямокутного паралелепіпеда проходять три площини, паралельні граням, які є площинами симетрії прямокутного паралелепіпеда.
Завдання.
1.Яку форму має основа правильної чотирикутної призми:
А) правильний трикутник ; Б)ромб ; В) квадрат ; г)прямокутник.
2.Чому дорівнює висота прямої трикутної призми:
А)ребру основи ; Б)бічному ребру ; В) діагоналі ; г) відразу визначити не можливо.
3.Скільки ребер має трикутна призма:
А) 3 ; Б)6 ; В) 9 ; г) 10.?
4.У прямій шестикутній призмі діагональний переріз має форму:
А) правильного трикутника ; Б)ромба ; В) квадрата ; г)прямокутника.
5.Висота правильної чотирикутної призми 8см, а діагональ основи 6 см. Чому дорівнює діагональ призми?
А) 8 см ; Б)10см ; В) 16см ; г) 14см.
6.Всі ребра трикутної призми дорівнюють по 3дм.Чому дорівнює площа бічної поверхні призми?
А) 9дм2 ; Б) 27дм2 ; В) 36дм2 ; г) 45дм2.
7.Віміри прямокутного паралелепіпеда дорівнюють 3см,2см, 6 см. Знайдіть довжину діагоналі паралелепіпеда:
А) 8см ; Б) 7см ; В)
Записати в робочий зошит тему
"Піраміда. Правильна та зрізана піраміди".
Переглянути презентацію по темі "Піраміда".
Переглянути презентацію по темі "Піраміда".
В робочий зошит записати відповіді на питання:
1. Який багатогранник називається пірамідою?
2. Назвіть основні елементи піраміди.
3. Яка піраміда називається правильною?
4. Властивості правильної піраміди.
5. Як знаходиться бічна поверхня правильної піраміди?
6. Яка піраміда називається зрізаною?
Д/завдання
1. Сторона основи правильної чотирикутної піраміди 6см, висота 4см.
Знайдіть повну поверхню піраміди.
2. Апофема правильної чотирикутної піраміди 5см, висота 3см.
Знайдіть повну поверхню піраміди.
Записуємо в робочий зошит тему
« Правильні багатогранники»
Переглянути відео за посиланням

Завдання:
1. Знайдіть площу повної поверхні октаедра, якщо площа
однієї грані дорівнює 2 дм2.
однієї грані дорівнює 2 дм2.
2. Знайдіть площу повної поверхні куба, якщо площа
однієї грані дорівнює 9 см2.
однієї грані дорівнює 9 см2.
3. Знайдіть площу повної поверхні куба, якщо його
ребро дорівнює 2 см.
ребро дорівнює 2 см.
4. Знайдіть площу повної поверхні правильного тетраедра,
ребро якого дорівнює 4 см.
ребро якого дорівнює 4 см.
5. Знайдіть діагональ куба, ребро якого дорівнює 1 дм.
Учням групи 212.
Урок: Розв’язування задач по темі "Багатогранники"
Мета уроку:
1) формувати навички застосовувати теоретичний матеріал до розв‘язування задач по даній темі, набути навичок творчо мислити;
2) розвивати логічне мислення, розвивати пошукову пізнавальну діяльність, розвивати самостійність;
Виконати завдання.
Виконати завдання.
1. У призмі площа бічної поверхні дорівнює 28 см2, а площа основи 12 см2. Знайдіть площу повної поверхні призми.
2. Чи є паралелепіпедом чотирикутна призма, в основі якої лежить чотирикутник, кути якого відповідно дорівнюють:
1) 30º, 150º, 30º, 150º; 2) 20º, 160º, 30º,150º?
3. Знайдіть площу бічної поверхні правильної п’ятикутної піраміди, якщо площа однієї бічної грані дорівнює 8 см2.
4. Бічне ребро похилої призми дорівнює 12 см і утворює з площиною основи кут 30º. Знайдіть висоту призми.
5. Сторони основи прямокутного паралелепіпеда дорівнюють 7 см і 24 см, а висота 5 см. Знайдіть площу:
1) діагонального перерізу паралелепіпеда;
2) повної поверхні паралелепіпеда.
6. Апофема правильної трикутної піраміди дорівнює 5 см, а сторона основи 6 см. Знайдіть площу повної поверхні піраміди.
7. Основою прямого паралелепіпеда є паралелограм з тупим кутом 150º і площею 15 см2. Площі бічних граней паралелепіпеда дорівнюють 20 см2 і 24 см2. Знайдіть висоту паралелепіпеда.
8. Ребро куба дорівнює 4 см. Площа повної поверхні куба дорівнює площі повної поверхні октаедра. Знайдіть площу однієї грані октаедра .
9. Основою піраміди є ромб з діагоналями 12 см і 16 см. Усі бічні грані піраміди утворюють з площиною основи кути по 45º. Знайдіть площу повної поверхні піраміди.
10. Двосхилий дах має форму тригранної призми. Він розміщений на будинку довжиною 21 м і шириною 8,5 м. Висота даху (підйом) — 3,2 м. Скільки квадратних метрів займає поверхня даху?
Д/з Повторити матеріал з теми "Багатогранники", підготуватися до тематичної контрольної роботи.
Учням групи 212.
Урок: Тематична контрольна робота з теми:
”Багатогранники”
1.Сторона куба дорівнює 10 см. Знайти площу поверхні куба.
А
|
Б
|
В
|
Г
|
600 см²
|
400 см²
|
800 см²
|
360 см²
|
2.Знайдіть площу поверхні прямокутного паралелепіпеда, виміри якого дорівнюють 2см, 3см і 4см.
А
|
Б
|
В
|
Г
|
24 см²
|
52 см²
|
18 см²
|
40 см²
|
3. Знайти діагональ прямокутного паралелепіпеда, виміри якого дорівнюють 2см, 3см і 6см.
А
|
Б
|
В
|
Г
|
5,5 см
|
36 см
|
11 см
|
7 см
|
4. Площа бічної грані правильної чотирикутної призми 48 см2, а периметр основи – 12 см. Яке твердження правильне?
А
|
Б
|
В
|
Г
|
Бічне ребро 4 см
|
Площа основи призми 9 см2
|
Площа діагонального перерізу 12 см2
|
Всі грані призми - квадрати
|
5. Основою прямої призми є прямокутний трикутник з гіпотенузою 10см і катетом 6см. Знайти площу бічної поверхні призми, якщо її бічне ребро дорівнює 5см.
А
|
Б
|
В
|
Г
|
120 см²
|
90 см²
|
180 см²
|
60 см²
|
6. Величина двогранного кута при бічному ребрі правильної трикутної призми дорівнює:
А
|
Б
|
В
|
Г
|
900
|
600
|
300
|
1200
|
7. В основі прямої призми лежить рівнобічна трапеція з основами 4см і 10см і бічною стороною 5см. Бічне ребро призми дорівнює 10см. Обчислити повну поверхню призми.
А
|
Б
|
В
|
Г
|
190 см²
|
296 см²
|
170 см²
|
186 см²
|
8. В основі прямої призми лежить прямокутник зі сторонами 6см і 8см. Знайдіть бічну поверхню призми, якщо площа її діагонального перерізу дорівнює 40см².
А
|
Б
|
В
|
Г
|
88 см²
|
480 см²
|
112 см²
|
56 см²
|
9. Сторона основи правильної трикутної піраміди дорівнює 4см, апофема 6см. Знайти площу бічної поверхні піраміди.
А
|
Б
|
В
|
Г
|
72 см²
|
24 см²
|
36 см²
|
48 см²
|
10. Апофема правильної трикутної піраміди 6 см, плоский кут при вершині 900. Яке твердження є правильним?
А
|
Б
|
В
|
Г
|
Бічна поверхня дорівнює
108 см2
|
Бічна поверхня дорівнює 54 см2
|
Висота піраміди 2 см.
|
Площа основи дорівнює площі бічної грані
|
11. Апофема правильної трикутної піраміди дорівнює 6см, а радіус кола, вписаного в її основу, дорівнює
А
|
Б
|
В
|
Г
|
36 см2
|
54 см2
|
72 см2
|
інша відповідь
|
12. Основою піраміди є прямокутник зі сторонами 6см і 8 см. Знайти висоту піраміди, якщо всі її бічні ребра рівні та дорівнюють 13см.
А
|
Б
|
В
|
Г
|
12 см
|
8 см
|
7 см
|
20см
|
Учням групи 212.
Урок: Розв’язування вправ та задач.
Початковий і середній рівень
1. Розв'яжіть нерівність: 0,6х ≤ 0,36.
А) (- ∞; 0,6); Б) [0,6; + ∞); В) (- ∞; 2]; Г) [2; + ∞).
2. Знайдіть значення виразу log 5 250 – log5 2.
А) 3; Б) 2; В) 1; Г) -3.
3. Коренем якого рівняння є число 16?
А) log 8 x = 2; Б) log 2 x = 8; В) log 4 x = 2; Г) log 4 x= 4.
4. Знайдіть похідну функції f(x) = 4х3+ 6х.
А) 12х2; Б) 12х2 + 6; В) 4х2 + 6х; Г) 4х4 + 6х2.
5. Знайдіть кутовий коефіцієнт дотичної, проведеної до графіка
функції f(х) = х2 – 1 у точці з абсцисою х0 = 3.
функції f(х) = х2 – 1 у точці з абсцисою х0 = 3.
А) 8; Б) 7; В) 6; Г) 2.
6. Яка функція не має критичних точок?
А) f (x) = x3; Б) f (x) = x3 + 1; В) f (x) = x3 + x; Г) f (x) = x3 + x2.
А) f (x) = x3; Б) f (x) = x3 + 1; В) f (x) = x3 + x; Г) f (x) = x3 + x2.
7. Точка рухається по закону s(t) = 1 + 2t2 (м).
Знайдіть швидкість руху точки в момент часу t =1с.
Знайдіть швидкість руху точки в момент часу t =1с.
А) 2 м/с; Б) 4 м/с; В) 3 м/с; Г) 5 м/с.
8. Який вектор колінеарний вектору (- 4; 18; 6)?
А) (2; 9; - 3); Б) (2; - 9; - 3); В) (2; - 9; 3); Г) (- 2; 9; - 3).
9. Точка С - середина відрізка АВ, А (2; 4; 6), С(0; 1; 10).
Знайдіть координати точки В.
А) В (1; 2,5; 8); Б) В (-2; -2; 14);
В) В (-2; -3; 4); Г) В (2; 6; 26).
10. Обчисліть площу бічної поверхні прямої призми, основою якої є паралелограм зі сторонами 8см і 22см, а висота призми дорівнює
15см.
10. Обчисліть площу бічної поверхні прямої призми, основою якої є паралелограм зі сторонами 8см і 22см, а висота призми дорівнює
15см.
А) 900 см2; Б) 450 см2; В) 600 см2; Г) 2640 см2.
11. При якому значенні n вектори a( 4; 2n - 1; - 1) і
b( 4; 9 - 3n; - 1) рівні?
А) - 2; Б) 8; В) 2; Г) - 8.
12. Знайдіть координати вектора МК, якщо М(2; 4; - 3) і К(8; 1; 0).
А) (10; 5; - 3); Б) (- 6; 3; - 3); В) (6; - 3; 3); Г) (16; 4; 0).
12. Знайдіть координати вектора МК, якщо М(2; 4; - 3) і К(8; 1; 0).
А) (10; 5; - 3); Б) (- 6; 3; - 3); В) (6; - 3; 3); Г) (16; 4; 0).
Достатній рівень
2.1. Знайдіть корінь рівняння: 9х+1 - 9х =24.
2.2. Знайдіть проміжки зростання функції f (x)= х3 – 3х2.
2.3. Знайдіть корені рівняння: log 2 x + log 2 (x - 3) = 2.
2.4. При якому значенні n вектори а(2; -1; n) і
b(4; n; -5) перпендикулярні?
2.5.Основа прямої призми - ромб з діагоналями 10см і 24см.
Менша діагональ призми дорівнює 26 см. Обчисліть площу
бічної поверхні призми.
Високий рівень
3.1. Розв’яжіть рівняння log 6 (x - 2) + log 6 (x - 1) = 1.
3.2 Дано трикутник АВС. Знайдіть зовнішній кут при вершині С, якщо
В(2;-1;-1), А(2;2;-4) і С(3;-1;-2).
В(2;-1;-1), А(2;2;-4) і С(3;-1;-2).
3.3. . Основою піраміди є правильний трикутник. Одна з бічних
граней піраміди перпендикулярна до площини основи, а дві інші нахилені до неї під кутом 600. Знайдіть об'єм піраміди, якщо її
висота дорівнює 12см.
граней піраміди перпендикулярна до площини основи, а дві інші нахилені до неї під кутом 600. Знайдіть об'єм піраміди, якщо її
висота дорівнює 12см.























Уроки завжли цікаві і доступні нашим учням.Успіхів Вам, Ларисо Миколаївно
ВідповістиВидалити