Шановні учні ВПУ№4 м.Хмельницького!
У ВПУ №4 м.Хмельницького з 12 березня по 11 травня 2020 року для здобувачів освіти запроваджено карантин.
В зв'язку з оголошенням карантину, ми переходимо на дистанційне навчання. Для подальшого вивчення математики після того як відкрили сторінку «Дистанційне навчання і курс», знайти свою групу, опрацювати матеріал, законспектувати і виконати завдання.
Виконані завдання та запитання надсилайте на електронну адресу: loravojtuk@gmail.com
Учням групи 113 і групи 114.
Записати в робочий зошит тему "Тригонометричні формули додавання та їх наслідки". Законспектувати формули .
Формули додавання
Формули подвійного аргументу

Переглянути відео за посилaнням
https://www.youtube.com/watch?v=_cOaTSIiO9k
Домашнє завдання Виконайте вправи
Домашнє завдання Виконайте вправи
1. Знайти знаачення виразу
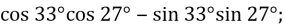
Учням групи 113
Контрольна робота.
ТЕМА : "Перпендикулярність прямих та площин".
І рівень
1.Прямі a і b перпендикулярні до площини. Яке взаємне розміщення цих прямих?
А
|
Б
|
В
|
перетинаються
|
мимобіжні
|
паралельні
|
2. Точка А належить площині α. Які з наведених тверджень є правильними?
I. Через точку А можна провести пряму, перпендикулярну до площини α.
II. Через точку А можна провести площину, перпендикулярну до площини α.
III. Через точку А можна провести площину, паралельну до площини α.
А
|
Б
|
В
|
Г
|
Д
|
лише I
|
лише II
|
лише I і II
|
лише II і III
|
I, II іIII
|
3. Точка А лежить поза площиною α. Скільки можна провести через точку А площин, які перпендикулярні до площини α?
А
|
Б
|
В
|
Г
|
Д
|
одну
|
дві
|
три
|
безліч
|
жодної
|
4. Пряма KO перпендикулярна до площини ромба ABCD, зображеного на рисунку. Укажіть кут між прямою BK і площиною ромба.
А
|
Б
|
В
|
Г
|
Д
|
ﮮOBK
|
ﮮCBK
|
ﮮBOK
|
ﮮBKO
|
ﮮABK
|
ІІ рівень
1. Точка B віддалена від площини β на 12см. Їз цієї точки проведено до площини β похилу BC. Знайдіть довжину похилої, якщо довжина її проекції на площину β дорівнює 5см.
А
|
Б
|
В
|
Г
|
Д
|
11 см
|
12 см
|
13 см
|
15 см
|
14 м
|
2
А
|
Б
|
В
|
Г
|
Д
|
MA
|
MD
|
MB
|
MC
|
AD
|
3.Із центра кола проведено перпендикуляр до її площини. Знайти діаметр кола, якщо довжина перпендикуляра 4 см, а відстань від його кінця до точок кола 5 см.
А
|
Б
|
В
|
Г
|
Д
|
6 см
|
3 см
|
2
|
8 см
|
4. Відстань від точки до площини дорівнює16 см. Знайти довжину похилої, якщо вона утворює з площиною кут 30о.
А
|
Б
|
В
|
Г
|
Д
|
25 см
|
30 см
|
32 см
|
35 см
|
55 см
|
ІІІ рівень
1.
2. Із точок А і В, які належать двом перпендикулярним площинам, проведено перпендикуляри АС та ВD на пряму перетину площин. Знайти довжину відрізка АВ, якщо АС = 3 см, ВD = 4 см, СD = 12 см
3. З точки, яка віддалена від площини на 2 см, проведено дві похилі, які утворюють з площиною кути 45о і 30о, а між собою прямий кут. Знайдіть відстань між основами похилих.
Учням групи 113 і 114
Переглянути відео за посиланням
Самостійна робота

Учням групи 113 і групи 114.
Записати в робочий зошит тему "Найпростіші тригонометричні рівняння".
Переглянути відео за посиланням

Записати формули в робочий зошит.
Переглянути відео за посиланням
Д/з
Установіть відповідність між рівняннями 1-3 та їхніми розв’язками
А-Г
А-Г
Учням групи 113 і 114
Записати в робочий зошит тему "Тригонометричні рівняння. Розв'язування вправ".
Переглянути відео за посиланням
Деякі способи розв’язування
тригонометричних рівнянь
1. Рівняння, що зводяться до квадратних:
Розв'яжіть рівняння: 6cos2x + 5sinx – 7 = 0.
Розв'язання
6cos2x + 5sinx – 7 = 0.
cos2x легко виразити через sin2x за допомогою основної тригонометричної тотожності cos2x + sin2x =1 => cos2x = 1 - sin2x;
Отже, 6(1 - sin2x) + 5sinx – 7 = 0;
Отже, 6(1 - sin2x) + 5sinx – 7 = 0;
6 - 6 sin2x+ 5sinx – 7 = 0;
6 sin2x - 5sinx + 1 = 0;
Нехай , sinx = y; отримаємо рівняння .
6y2 - 5y + 1 =0;
Нехай , sinx = y; отримаємо рівняння .
6y2 - 5y + 1 =0;
D = b2 – 4ac = (-5)2 - 4·6·1 = 25 -24 = 1;
y1 = ½ ; y2 = 1/3;
1) sinx = 1/2; x = (-1)k π/6 + πk, k Є Z.
2) sinx = 1/3; x = (-1)k arcsin1/3 + π, k Є Z.
1) sinx = 1/2; x = (-1)k π/6 + πk, k Є Z.
2) sinx = 1/3; x = (-1)k arcsin1/3 + π, k Є Z.
Відповідь: x = (-1)k π/6 + πk, k Є Z; x = (-1)k arcsin1/3 + π, k Є Z.
2. Спосіб розкладання на множники:
Розв'яжіть рівняння
Розв'яжіть рівняння
Розв'язання
1- cos8x = sin4x;
1- cos(2·4x) = sin4x;
1 - (1 – 2sin24x) = sin4x;
1 – 1 + 2sin24x = sin4x;
2sin2 4x = sin4x;
2sin2 4x - sin4x = 0;
sin4x · (2sin4x - 1) = 0;
sin4x = 0 або 2sin4x – 1 = 0
4x = πn, n Є Z 2sin4x = 1
x = (πn)/4, n Є Z sin4x = 1/2
4x = (-1)k π/6 + πk, k Є Z
x = (-1)k π/24 + (πk)/4, k Є Z
Відповідь: x = (πn)/4, n Є Z; x = (-1)k π/24 + (πk)/4, k Є Z.
Виконання вправ
Розв'яжіть рівняння:
1. 2sin3x – 1 = 0;
2. 2cosx – sin2xcosx = 0;
3. sinxcos2x = 3sinx;
4. 4cos2x + 4sinx – 1 = 0;
5. 2cos2x + cosx – 1 = 0.
Учням групи 113 і 114
Тема уроку : Розв'язування найпростіших тригонометричних нерівностей.
Мета уроку: Формування умінь розв'язувати найпростіші тригонометричні нерівності: sin t > a, sin t < a, cos t > a, cos t < a, tg t > a, tg t < a, ctg t > a,ctg t
I. Сприймання і усвідомлення розв'язування найпростіших тригонометричних нерівностей.
Нерівність називається тригонометричною, якщо вона містить змінну тільки під знаком тригонометричної функції. Наприклад, sin 3x > 1, cos x + tg x < 1 — тригонометричні нерівності. Розв'язати тригонометричну нерівність означає знайти множину значень змінної, при яких нерівність виконується.
Розв'язування тригонометричних нерівностей зводиться до розв'язування нерівностей:
sin x > a, sin x < a,
cos x > a, cos x < a,
tg x > a, tg x < a,
сtg x > a, сtg x < a,
які називаються найпростішими.
ІІ Переглянути відео за посиланням
https://www.youtube.com/watch?v=Jb92Ds1Tg90
https://www.youtube.com/watch?v=F-Qfqv_o5yU
Д/з Опрацювати конспект та виконати завдання в зошиті.
Розв'язати нерівність
1. cos x > 1/2
2. sin x > -1/2
3. tg x < 1
4. ctg x > -1
5.cos 2x < 1
6. sin(x + π) < 1
7. tg 3x > -1
Учням групи 113 і групи 114
Тематична
контрольна робота по темі :
Підсумкова контрольна робота
з математики
за 2019-2020 навчальний рік
Початковий і середній рівень
1. Яку з наведених властивостей має функція у = 3 - х2?
А) cпадає на множині R; Б) парна;
В) зростає на множині R; Г) непарна. 2.Подайте у вигляді степеня вираз (а2/3)12.
А) cпадає на множині R; Б) парна;
В) зростає на множині R; Г) непарна. 2.Подайте у вигляді степеня вираз (а2/3)12.
А) а6; Б) а21; В) а8; Г) а16.
3. Діагоналі трапеції паралельні площині α.
Як розташовані площина α і площина трапеції?
А) паралельні; Б) перетинаються;
В) перпендикулярні; Г) визначити неможливо.
4. Ціну товару знизили на 20% і він став коштувати 124 грн.
Якою була початкова ціна товару?
А) 155 грн; Б) 180 грн; В) 540 грн; Г) 620 грн.
5. Визначити знак виразу: sin 1570 cos 2190.
А) sin 1570 cos 2190 > 0; Б) sin 1570 cos 2190 <0;
В) sin 1570 cos 2190 = 0; Г) визначити неможливо.
6. Спростити вираз tgα · cosα.
А) sin α; Б) cos α; В) 1/cos α; Г) 1.
7. Вибрати вірне твердження.
А) Через пряму і точку можна провести площину, і тільки одну.
Б) Ортогональною проекцією трапеції на площину може бути
прямокутник.
В) Кут між мимобіжними прямими це кут між прямими, які
перетинаються і паралельні даним мимобіжним прямим.
Г) Через точку поза площиною можна провести безліч
площин паралельних даній площині.
8. Спростити вираз sin 4α cos α - cos 4α sin α.
А) sin 3α; Б) cos 4α; В) sin 5α; Г) cos 5α.
9. Розв’язати рівняння: х4 = 81.
А) 3; Б) -3; В) -3; 3; Г) -9; 9.
10. Графік якої функції зображено на малюнку?
А) y = - x/6; Б) y = -6x;
В) y = -6/x; Г) y = 6x.
11. Розв’язати рівняння : sin x=3.
А) arcsin3 + πn, n є Z; Б) (-1)n3+πn, n є Z ;
В) (-1)n arcsin3+3πn, n є Z; Г) інша відповідь.
12. Точка M рівновіддалена від усіх вершин прямокутного
трикутника, MO — перпендикуляр до площини цього
трикутника. Де розташована точка O?
А) Точка О збігається з вершиною прямого кута.
Б) Точка О – центр вписаного кола.
В) Точка О належить одному з катетів.
Г Точка О -- середина гіпотенузи.
Достатній рівень
2.1 Розв’язати рівняння : (x + 8)1/2 = х – 4.
2.2 Спростити вираз : (1+ tgα)2 +(1 - tgα)2 .
2.3 Площина α перетинає сторону AB трикутника ABC у точці M,
сторону AC — у точці P і паралельна стороні BC. Знайдіть
довжину сторони BC, якщо AM = 6 см, BM = 9 см, MP = 4 см.
2.4 . Із точки до площини проведено дві похилі, що дорівнюють
якщо проекції похилих відносяться як 2:3.
Високий рівень
3.1 Розв’язати рівняння: cos x- cos 2x =0 .
3.2 З точки А до площини α проведено дві рівні похилі по 4 см
кожна. Кут між похилими дорівнює 600, а кут між їхніми
проекціями – прямий. Знайдіть відстань від точки А до площини α.
Записати в робочий зошит тему "Найпростіші тригонометричні рівняння".
Переглянути відео за посиланням
Записати формули в робочий зошит.
Переглянути відео за посиланням
Д/з 1. Розв’яжіть рівняння
2. Установіть відповідність між рівняннями 1-3 та їхніми розв’язками А-Г

Учням групи 115
Записати в робочий зошит тему "Тригонометричні рівняння. Розв'язування вправ".
Переглянути відео за посиланням
Деякі способи розв’язування
тригонометричних рівнянь
1. Рівняння, що зводяться до квадратних:
Розв'яжіть рівняння: 6cos2x + 5sinx – 7 = 0.
Розв'язання
6cos2x + 5sinx – 7 = 0.
cos2x легко виразити через sin2x за допомогою основної тригонометричної тотожності cos2x + sin2x =1 => cos2x = 1 - sin2x;
Отже, 6(1 - sin2x) + 5sinx – 7 = 0;
Отже, 6(1 - sin2x) + 5sinx – 7 = 0;
6 - 6 sin2x+ 5sinx – 7 = 0;
6 sin2x - 5sinx + 1 = 0;
Нехай , sinx = y; отримаємо рівняння .
6y2 - 5y + 1 =0;
Нехай , sinx = y; отримаємо рівняння .
6y2 - 5y + 1 =0;
D = b2 – 4ac = (-5)2 - 4·6·1 = 25 -24 = 1;
y1 = ½ ; y2 = 1/3;
1) sinx = 1/2; x = (-1)k π/6 + πk, k Є Z.
2) sinx = 1/3; x = (-1)k arcsin1/3 + π, k Є Z.
1) sinx = 1/2; x = (-1)k π/6 + πk, k Є Z.
2) sinx = 1/3; x = (-1)k arcsin1/3 + π, k Є Z.
Відповідь: x = (-1)k π/6 + πk, k Є Z; x = (-1)k arcsin1/3 + π, k Є Z.
2. Спосіб розкладання на множники:
Розв'яжіть рівняння
Розв'яжіть рівняння
Розв'язання
1- cos8x = sin4x;
1- cos(2·4x) = sin4x;
1 - (1 – 2sin24x) = sin4x;
1 – 1 + 2sin24x = sin4x;
2sin2 4x = sin4x;
2sin2 4x - sin4x = 0;
sin4x · (2sin4x - 1) = 0;
sin4x = 0 або 2sin4x – 1 = 0
4x = πn, n Є Z 2sin4x = 1
x = (πn)/4, n Є Z sin4x = 1/2
4x = (-1)k π/6 + πk, k Є Z
x = (-1)k π/24 + (πk)/4, k Є Z
Відповідь: x = (πn)/4, n Є Z; x = (-1)k π/24 + (πk)/4, k Є Z.
Виконання вправ
Розв'яжіть рівняння:
1. 2sin3x – 1 = 0;
2. 2cosx – sin2xcosx = 0;
3. sinxcos2x = 3sinx;
4. 4cos2x + 4sinx – 1 = 0;
5. 2cos2x + cosx – 1 = 0.
Учням групи 115
ІІ Переглянути відео за посиланням
Д/з Опрацювати конспект та виконати завдання в зошиті.
Учням групи 115
Тема уроку : Розв'язування найпростіших тригонометричних нерівностей.
Мета уроку: Формування умінь розв'язувати найпростіші тригонометричні нерівності: sin t > a, sin t < a, cos t > a, cos t < a, tg t > a, tg t < a, ctg t > a,ctg t
I. Сприймання і усвідомлення розв'язування найпростіших тригонометричних нерівностей.
Нерівність називається тригонометричною, якщо вона містить змінну тільки під знаком тригонометричної функції. Наприклад, sin 3x > 1, cos x + tg x < 1 — тригонометричні нерівності. Розв'язати тригонометричну нерівність означає знайти множину значень змінної, при яких нерівність виконується.
Розв'язування тригонометричних нерівностей зводиться до розв'язування нерівностей:
sin x > a, sin x < a,
cos x > a, cos x < a,
tg x > a, tg x < a,
сtg x > a, сtg x < a,
які називаються найпростішими.
ІІ Переглянути відео за посиланням
Д/з Опрацювати конспект та виконати завдання в зошиті.
Домашня самостійна робота
Розв'язати нерівність
Розв'язати нерівність
1. cos x > 1/2
2. sin x > -1/2
3. tg x < 1
4. ctg x > -1
5.cos 2x < 1
6. sin(x + π) < 1
7. tg 3x > -1
Учням групи 115
Підсумкова контрольна робота
з математики
за 2019-2020 навчальний рік
Початковий і середній рівень
1. Яку з наведених властивостей має функція у = 3 - х2?
А) cпадає на множині R; Б) парна;
В) зростає на множині R; Г) непарна. 2.Подайте у вигляді степеня вираз (а2/3)12.
А) cпадає на множині R; Б) парна;
В) зростає на множині R; Г) непарна. 2.Подайте у вигляді степеня вираз (а2/3)12.
А) а6; Б) а21; В) а8; Г) а16.
3. Діагоналі трапеції паралельні площині α.
Як розташовані площина α і площина трапеції?
А) паралельні; Б) перетинаються;
В) перпендикулярні; Г) визначити неможливо.
4. Ціну товару знизили на 20% і він став коштувати 124 грн.
Якою була початкова ціна товару?
А) 155 грн; Б) 180 грн; В) 540 грн; Г) 620 грн.
5. Визначити знак виразу: sin 1570 cos 2190.
А) sin 1570 cos 2190 > 0; Б) sin 1570 cos 2190 <0;
В) sin 1570 cos 2190 = 0; Г) визначити неможливо.
6. Спростити вираз tgα · cosα.
А) sin α; Б) cos α; В) 1/cos α; Г) 1.
7. Вибрати вірне твердження.
А) Через пряму і точку можна провести площину, і тільки одну.
Б) Ортогональною проекцією трапеції на площину може бути
прямокутник.
В) Кут між мимобіжними прямими це кут між прямими, які
перетинаються і паралельні даним мимобіжним прямим.
Г) Через точку поза площиною можна провести безліч
площин паралельних даній площині.
8. Спростити вираз sin 4α cos α - cos 4α sin α.
А) sin 3α; Б) cos 4α; В) sin 5α; Г) cos 5α.
9. Розв’язати рівняння: х4 = 81.
А) 3; Б) -3; В) -3; 3; Г) -9; 9.
10. Графік якої функції зображено на малюнку?
А) y = - x/6; Б) y = -6x;
В) y = -6/x; Г) y = 6x.
11. Розв’язати рівняння : sin x=3.
А) arcsin3 + πn, n є Z; Б) (-1)n3+πn, n є Z ;
В) (-1)n arcsin3+3πn, n є Z; Г) інша відповідь.
12. Точка M рівновіддалена від усіх вершин прямокутного
трикутника, MO — перпендикуляр до площини цього
трикутника. Де розташована точка O?
А) Точка О збігається з вершиною прямого кута.
Б) Точка О – центр вписаного кола.
В) Точка О належить одному з катетів.
Г Точка О -- середина гіпотенузи.
Достатній рівень
2.1 Розв’язати рівняння : (x + 8)1/2 = х – 4.
2.2 Спростити вираз : (1+ tgα)2 +(1 - tgα)2 .
2.3 Площина α перетинає сторону AB трикутника ABC у точці M,
сторону AC — у точці P і паралельна стороні BC. Знайдіть
довжину сторони BC, якщо AM = 6 см, BM = 9 см, MP = 4 см.
2.4 . Із точки до площини проведено дві похилі, що дорівнюють
якщо проекції похилих відносяться як 2:3.
Високий рівень
3.1 Розв’язати рівняння: cos x- cos 2x =0 .
3.2 З точки А до площини α проведено дві рівні похилі по 4 см
кожна. Кут між похилими дорівнює 600, а кут між їхніми
проекціями – прямий. Знайдіть відстань від точки А до площини α.
.

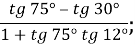
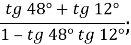





Немає коментарів:
Дописати коментар