Дистанційне навчання гр 203, 204, 207.

  

Шановні учні ВПУ№4 м.Хмельницького!

У  ВПУ №4 м.Хмельницького з 12 березня по 11 травня 2020 року для здобувачів освіти запроваджено  карантин.
В зв'язку з оголошенням карантину, ми переходимо на дистанційне навчання. Для подальшого вивчення математики після того як відкрили сторінку «Дистанційне навчання і курс», знайти свою групу, опрацювати матеріал, законспектувати і виконати завдання.


Виконані завдання та запитання надсилайте на електронну адресу: loravojtuk@gmail.com


   Учням групи 203     

    Записати в робочий зошит тему  

   "Піраміда. Правильна та зрізана піраміди".  

    Переглянути презентацію по темі     "Піраміда".   














 











 








В робочий зошит  записати відповіді на питання:

1.  Який багатогранник називається пірамідою?
2.  Назвіть основні елементи піраміди.
3.  Яка піраміда називається правильною?
4. Властивості правильної піраміди.
5. Як знаходиться бічна поверхня правильної піраміди?
6. Яка піраміда називається зрізаною? 


 Учням  групи   203.
Записуємо в робочий зошит тему
« Паралелепіпед. Прямокутний паралелепіпед»

       Паралелепіпед — це призма, основою якої є паралелограм.
Протилежні грані паралелепіпеда паралельні і рівні.
Діагоналі паралелепіпеда перетинаються в одній точці і діляться нею навпіл.

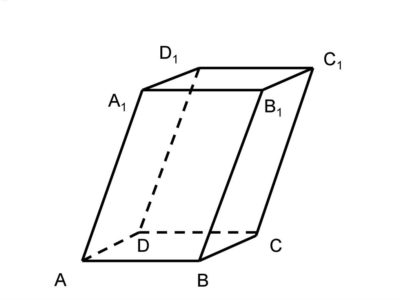
Картинки по запросу "Паралелепіпед ."

     Прямий паралелепіпед  - це паралелепіпед, що має перпендикулярні до основ бічні ребра.
  Прямокутний паралелепіпед — прямий паралелепіпед , основою якого є прямокутник.
    Бічні грані прямокутного паралелепіпеда перпендикулярні його основам. 
 Лінійними розмірами прямокутного паралелепіпеда є довжини його непаралельних ребер. Прямокутний паралелепіпед, усі лінійні розміри якого рівні, називається кубом. 

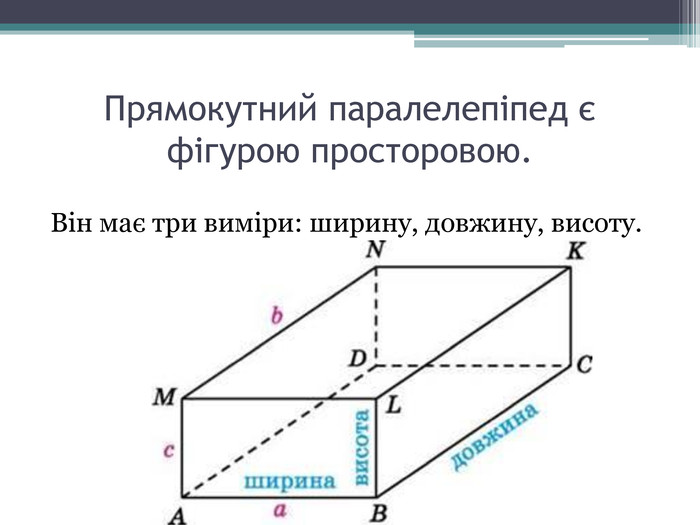
Картинки по запросу "Паралелепіпед ."


Діагоналі прямокутного паралелепіпеда рівні.
Усі двогранні кути прямокутного паралелепіпеда – прямі.
Квадрат будь-якої діагоналі прямокутного паралелепіпеда є сумою квадратів трьох його вимірів.
Точка перетину діагоналей паралелепіпеда є його центром симетрії.Через центр симетрії прямокутного паралелепіпеда проходять три площини, паралельні граням, які є площинами симетрії прямокутного паралелепіпеда.
Картинки по запросу "Паралелепіпед ."












Тестові завдання
1) У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює:

А) Добутку трьох його вимірів.
Б). Сумі квадратів лінійних розмірів.
В) Сумі квадратів трьох його вимірів.
Г) Частці його лінійних розмірів.
Д) Різниці квадратів його вимірів.

2) Якщо ребро куба дорівнює 3 см, то його повна площа поверхні дорівнює:
А) 3 см.
Б) 27 см
В) 54 см
Г) 36 см
Д) 9 см

3) Якщо виміри прямокутного паралелепіпеда 3 см, 2 см та 6 см, то площа найбільшої грані дорівнює:
А) 16 см
Б) 14 см
В) 18 см
Г) 12 см
Д) 6 см

4) Висота похилої призми удвічі коротша за бічне ребро. Який кут утворює висота призми із цим бічним ребром?
А) 30º;
Б) 15º;
В) 75º;
Г) 60º;
Д) 45º.
План-конспект уроку - Сайт вчителя математики та фізики
5) На малюнку зображено прямокутний паралелепіпед АВСDА1В1С1D1, АВ = 1, АD= 2, АА1= 2.                                                                         Установити відповідність між геометричними величинами (1-4) та їхніми числовими значеннями  (А-Д).





1.  Відстань між мимобіжними прямими               
АА1 і DС.
2.  Довжина діагоналі прямокутного
паралелепіпеда.
3.  Площа повної поверхні прямокутного
паралелепіпеда.
4.  Площа бічної поверхні прямокутного
паралелепіпеда.
А 16.           Б 12.         В 4.         Г 3.       Д 2.

6)  В основі прямої призми лежить прямокутник зі стороною 8 см і діагоналлю 10 см. Бічне ребро призми дорівнює 10 см. Знайдіть повну поверхню призми. 
7) Основа прямої призми — прямокутний трикутник з катетом 4 см і гіпотенузою 5 см. Висота призми дорівнює 6 см. Знайдіть площу повної поверхні призми. 

Виконання вправ.

1. Бічна грань правильної шестикутної призми – квадрат, площа якого дорівнює 36см². Обчислити периметр основи призми.   
2. Площа бічної грані правильної трикутної призми дорівнює 24см², а периметр основи – 9см. Знайти бічне ребро призми.  
3. Основою прямої призми є ромб із діагоналями 10см і 24см. Знайти висоту призми, якщо менша діагональ призми дорівнює 26см.
4. Сторона основи правильної чотирикутної піраміди 6см, висота 4см. Знайдіть повну поверхню піраміди.
5. Апофема правильної чотирикутної піраміди 5см, висота 3см. Знайдіть повну поверхню піраміди. 

Учням  групи   203.


 Записуємо в робочий зошит тему
« Правильні багатогранники»

     Переглянути відео за посиланням






Завдання:
1. Знайдіть площу повної поверхні октаедра, якщо площа 
    однієї грані дорівнює  2 дм2.
2. Знайдіть площу повної поверхні куба, якщо площа 
    однієї грані  дорівнює   9 см2.
3. Знайдіть площу повної поверхні куба, якщо його 
    ребро дорівнює  2 см.   
4. Знайдіть площу повної поверхні правильного тетраедра, 
    ребро  якого  дорівнює 4 см.
5. Знайдіть діагональ куба, ребро якого дорівнює 1 дм.



Учням  групи   203.
Урок:  Розв’язування задач по темі "Багатогранники"
Мета уроку:


1) формувати навички застосовувати теоретичний матеріал до розв‘язування задач по даній темі, набути навичок творчо мислити;

2) розвивати логічне мислення,  розвивати пошукову пізнавальну діяльність, розвивати самостійність;


Виконати завдання.
1. У призмі площа бічної поверхні дорівнює 28 см2, а площа основи 12 см2. Знайдіть площу повної поверхні призми.
2. Чи є паралелепіпедом чотирикутна призма, в основі якої лежить чотирикутник, кути якого відповідно дорівнюють:
1) 30º, 150º, 30º, 150º;     2) 20º, 160º, 30º,150º?
3. Знайдіть площу бічної поверхні правильної п’ятикутної піраміди, якщо площа однієї бічної грані дорівнює 8 см2.
4. Бічне ребро похилої призми дорівнює 12 см і утворює з площиною основи кут 30º. Знайдіть висоту призми.
5. Сторони основи прямокутного паралелепіпеда  дорівнюють 7 см і 24 см, а висота 5 см. Знайдіть площу:
1) діагонального перерізу паралелепіпеда;
2) повної поверхні паралелепіпеда.
6. Апофема правильної трикутної  піраміди дорівнює 5 см, а сторона основи 6 см. Знайдіть площу повної поверхні піраміди.
7. Основою прямого паралелепіпеда є паралелограм з тупим кутом 150º  і площею 15 см2. Площі бічних граней паралелепіпеда дорівнюють 20 см2 і 24 см2. Знайдіть висоту паралелепіпеда.
8. Ребро куба дорівнює 4 см. Площа повної поверхні куба дорівнює площі повної поверхні октаедра. Знайдіть площу однієї грані октаедра .
9. Основою піраміди є ромб з діагоналями 12 см і 16 см. Усі бічні грані піраміди утворюють з площиною основи кути по 45º. Знайдіть площу повної поверхні піраміди.
10. Двосхилий дах має форму тригранної призми. Він розміщений на будинку довжиною 21 м і шириною 8,5 м. Висота даху (підйом) — 3,2 м. Скільки квадратних метрів займає поверхня даху?

Д/з  Повторити  матеріал з теми "Багатогранники",  підготуватися до тематичної контрольної роботи. 


Учням  групи   203.
  Урок:  Тематична контрольна робота з  теми:
”Багатогранники”                      
    1.Сторона куба дорівнює 10 см. Знайти площу поверхні куба.
А
Б
В
Г
600 см²
400 см²
800 см²
360 см²

2.Знайдіть площу поверхні прямокутного паралелепіпеда, виміри якого               дорівнюють 2см, 3см і 4см.
А
Б
В
Г
24 см²
52 см²
18 см²
40 см²

3. Знайти діагональ прямокутного паралелепіпеда, виміри якого дорівнюють     2см, 3см і 6см.
А
Б
В
Г
5,5 см
36 см
11 см
7 см

4. Площа бічної грані правильної чотирикутної призми 48 см2, а периметр      основи – 12 см. Яке твердження правильне?
    
А
Б
В
Г
     Бічне ребро 4 см
Площа основи     призми 9 см2
     Площа діагонального перерізу 12 см2
     Всі грані призми - квадрати
5. Основою прямої призми є прямокутний трикутник з гіпотенузою 10см і катетом  6см. Знайти площу бічної поверхні призми, якщо її бічне ребро дорівнює 5см.
А
Б
В
Г
120 см²
90 см²
180 см²
60 см²

6. Величина двогранного кута при бічному ребрі правильної трикутної   призми дорівнює:
А
Б
В
Г
900
600
300
1200

7. В основі прямої призми лежить рівнобічна трапеція з основами 4см і 10см і бічною стороною 5см. Бічне ребро призми дорівнює 10см. Обчислити повну поверхню призми.
А
Б
В
Г
190 см²
296 см²
170 см²
186 см²

8. В основі прямої призми лежить прямокутник зі сторонами 6см і 8см.     Знайдіть бічну поверхню призми, якщо площа її діагонального перерізу дорівнює 40см².
А
Б
В
Г
88 см²
480 см²
112 см²
56 см²

9. Сторона основи правильної трикутної піраміди дорівнює 4см, апофема   6см. Знайти площу бічної поверхні піраміди. 
А
Б
В
Г
72 см²
24 см²
36 см²
48 см²

10.  Апофема правильної трикутної піраміди 6 см, плоский кут при вершині  900. Яке твердження є правильним?

А
Б
В
Г
    Бічна поверхня дорівнює
108 см2
Бічна поверхня дорівнює 54 см2
     Висота піраміди   2 см.
Площа основи дорівнює площі бічної грані

11. Апофема правильної трикутної піраміди дорівнює 6см, а радіус кола,   вписаного в її основу, дорівнює  см. Обчисліть бічну поверхню піраміди.

А
Б
В
Г
36 см2
54 см2
72 см2
інша відповідь

12. Основою піраміди є прямокутник зі сторонами 6см і 8 см. Знайти висоту   піраміди, якщо всі її бічні ребра рівні та дорівнюють 13см.
А
Б
В
Г
12 см
8 см
7 см
20см


         Учням  групи   203.

                  Підсумкова контрольна робота.
Початковий і середній рівень
1. Розв'яжіть нерівність:  0,6х  ≤  0,36.
А) (- ∞; 0,6);  Б) [0,6; + ∞);  В) (- ∞; 2];     Г) [2; + ∞).
2. Знайдіть похідну функції     f(x) = 4х3+ 6х.
А) 12х2;     Б) 12х2 + 6;    В) 4х2 + 6х;     Г) 4х4 + 6х2.
3. Знайдіть кутовий коефіцієнт дотичної, проведеної до графіка функції f(х) = х2 – 1 у точці з абсцисою х0 = 3.
А) 8;     Б) 7;     В) 6;     Г) 2.
4. Яка функція не має критичних точок?
А)  f (x) = x3;   Б) f (x) = x3 + 1;   В) f (x) = x3 + x;   Г) f (x) = x3 + x2.
5. Точка рухається по закону s(t) = 1 + 2t2 (м). Знайдіть швидкість руху точки в момент         часу t =1с.
А) 2 м/с;     Б) 4 м/с;    В) 3 м/с;     Г) 5 м/с.
6. Яка з точок лежить на осі абсцис?
А) (0; 3; - 1);     Б) (0; 0; 7);     В) (0; - 1; 0);     Г) (2; 0; 0).
7. Точка С - середина відрізка АВ,  А (2; 4; 6), С(0; 1; 10).
Знайдіть координати точки В.
А) В (1; 2,5; 8);     Б) В (-2; -2; 14);     В) В (-2; -3; 4);     Г) В (2; 6; 26).
8. Який вектор колінеарний вектору (- 4; 18; 6)?
А) (2; 9; - 3);     Б) (2; - 9; - 3);     В) (2; - 9; 3);     Г) (- 2; 9; - 3).
9. Обчисліть площу бічної поверхні прямої призми, основою якої є паралелограм зі сторонами 8 см і 22 см, а висота призми дорівнює 15см.
А) 900 см2;      Б) 450 см2;     В) 600 см2;     Г) 2640 см2.
10. При  якому значенні n вектори  a ( 4; 2n - 1; - 1) і b ( 4; 9 - 3n; - 1) рівні?
А) - 2;     Б) 8;     В) 2;     Г) - 8.
11. Знайдіть координати вектора МК, якщо М(2; 4; - 3) і К(8; 1; 0).
А)  (10; 5; - 3);     Б) (- 6; 3; - 3);     В) (6; - 3; 3);     Г) (16; 4; 0).
12. Довжина похилої проведеної з точки A на площину α дорівнює 10см, проекція цієї похилої на площину α дорівнює 8см. Знайдіть відстань від точки А до площини α.
А) 2см;     Б) 6см;     В) 3см;     Г) 9см.
Достатній рівень
2.1. Знайдіть корінь рівняння:     9х+1 - 9х =24.
2.2.  Знайдіть проміжки зростання функції  f (x)= х3 – 3х2.
2.3. З точки до прямої проведено дві похилі завдовжки  25 см і 17 см. Знайдіть довжини проекцій цих похилих на дану пряму, якщо вони відносяться як 5 : 2.
2.4. При якому значенні n вектори а(2; -1; n) і b(4; n; -5) перпендикулярні?
2.5. Основа прямої призми - ромб з діагоналями 10 см і 24 см. Менша діагональ призми дорівнює 26 см. Обчисліть площу бічної поверхні призми.
2.6.  Скат двоскатного даху утворює з площиною стелі кут 45. Ширина даху 18м. На який висоті від стелі знаходиться коньок даху?
Високий рівень
11. Розв’яжіть рівняння 2 ∙ 25х  - 5 ∙ 4х = 3 ∙ х10
12. З точки А до площини α проведено дві рівні похилі по 4 см кожна. Кут між похилими дорівнює 600, а кут між їхніми проекціями – прямий. Знайдіть відстань від точки А до площини α.
13. . Основою піраміди є правильний трикутник. Одна з бічних граней піраміди перпендикулярна до площини основи, а дві інші нахилені до неї під кутом 600. Знайдіть об'єм піраміди, якщо її висота дорівнює 12см.


 Для учнів 204 групи
   Записуємо в робочий зошит тему
  «Вектори у просторі» 

  Переглянути відео за посиланням


  Переглянути презентацію


1844 -1850 р.р. - основи векторного числення були закладені дослідженнями англійського математика У.Гамільтона і німецького математика Г. Грассмана по гіперкомплексних числах.

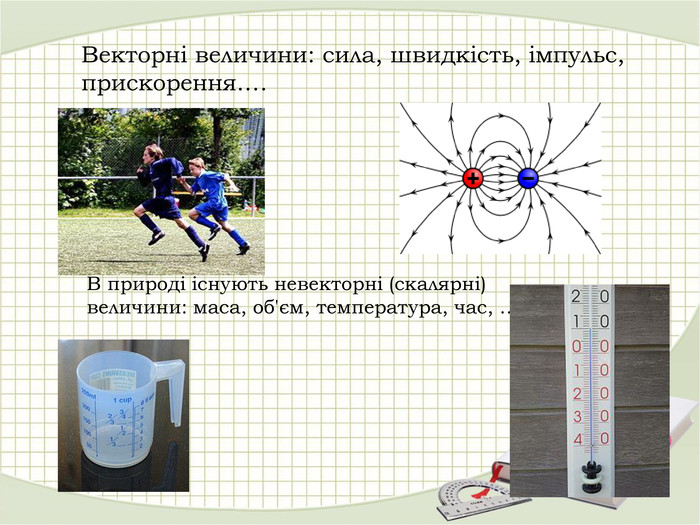
 Векторні величини: сила, швидкість, імпульс, прискорення…. В природі існують невекторні (скалярні) величини: маса, об'єм, температура, час, …..

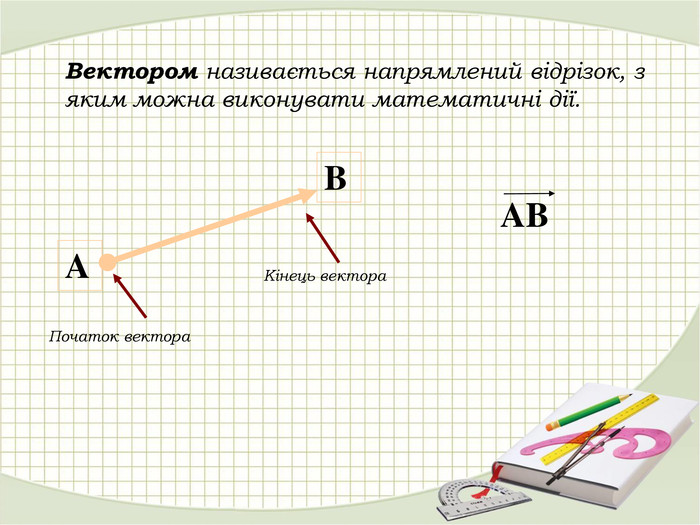
Вектором називається напрямлений відрізок, з яким можна виконувати математичні дії. A B Початок вектора Кінець вектора AB

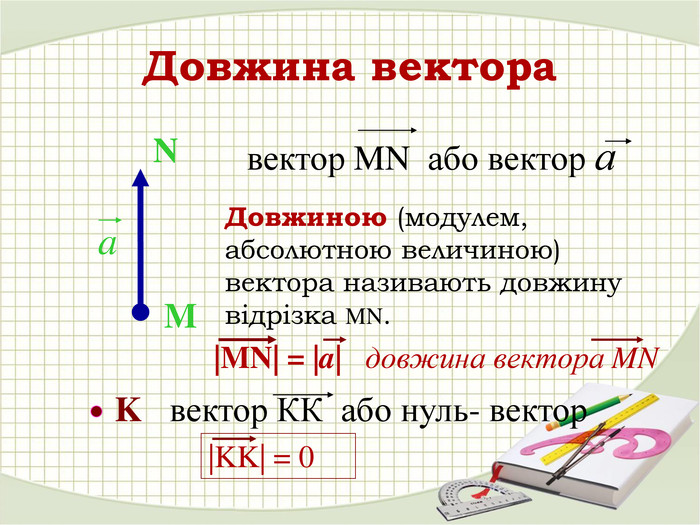
K Довжина вектора M N a вектор MN або вектор а вектор КК або нуль- вектор Довжиною (модулем, абсолютною величиною) вектора називають довжину відрізка MN. |MN| = |a| довжина вектора MN |KK| = 0

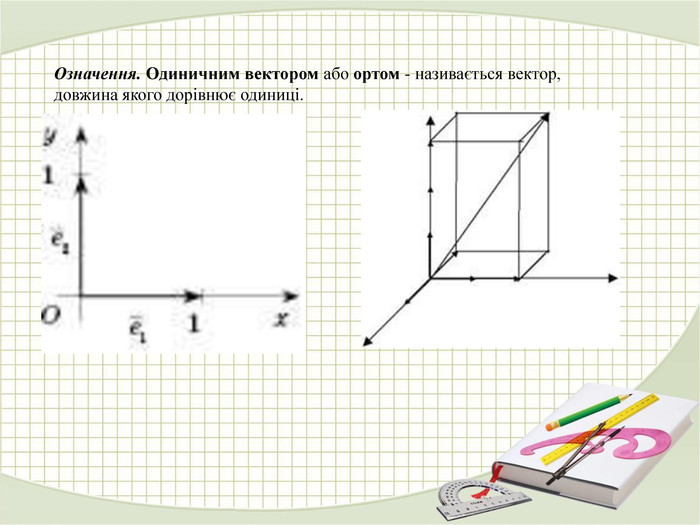
Означення. Одиничним вектором або ортом - називається вектор, довжина якого дорівнює одиниці.

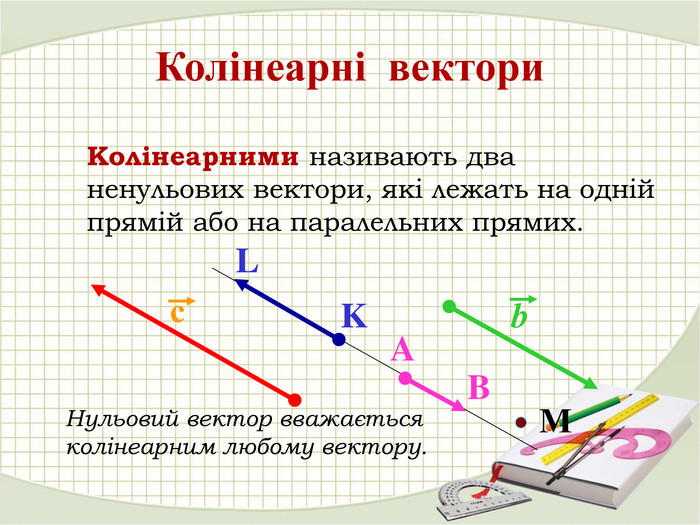
Нульовий вектор вважається колінеарним любому вектору. Колінеарні вектори М с L K b A B Колінеарними називають два ненульових вектори, які лежать на одній прямій або на паралельних прямих.
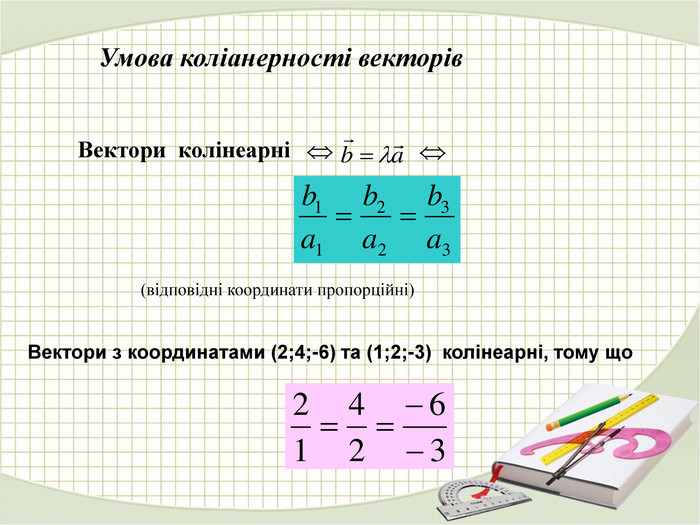
(відповідні координати пропорційні) Вектори колінеарні Вектори з координатами (2;4;-6) та (1;2;-3) колінеарні, тому що Умова коліанерності векторів

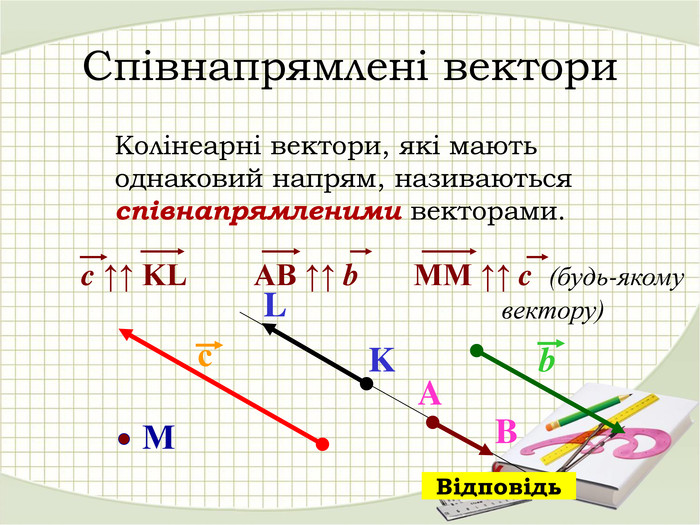
с L K b A B Співнапрямлені вектори Колінеарні вектори, які мають однаковий напрям, називаються співнапрямленими векторами. М c ↑↑ KL AB ↑↑ b MM ↑↑ c (будь-якому вектору) Відповідь
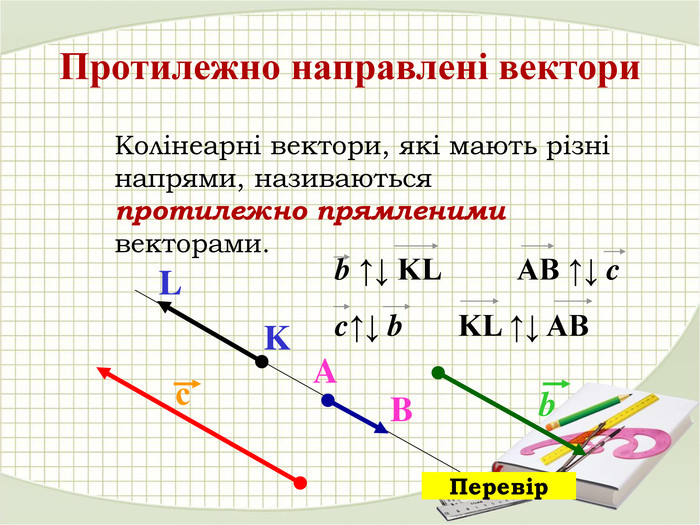
с b L K A B Протилежно направлені вектори b ↑↓ KL AB ↑↓ c c↑↓ b KL ↑↓ AB Перевір Колінеарні вектори, які мають різні напрями, називаються протилежно прямленими векторами.

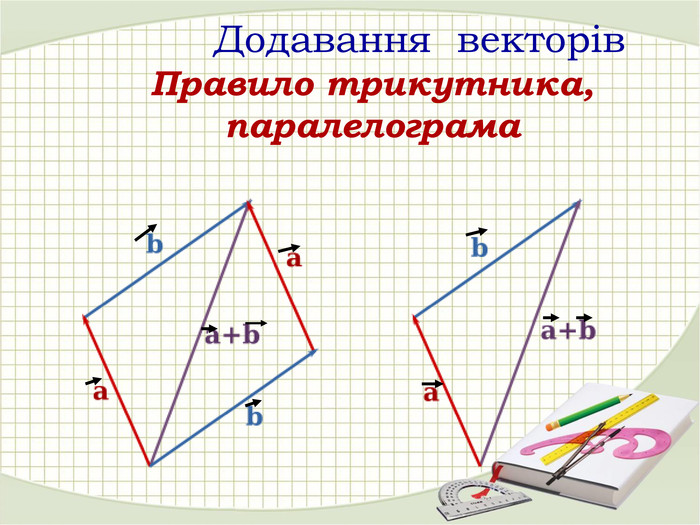
Додавання векторів Правило трикутника, паралелограма

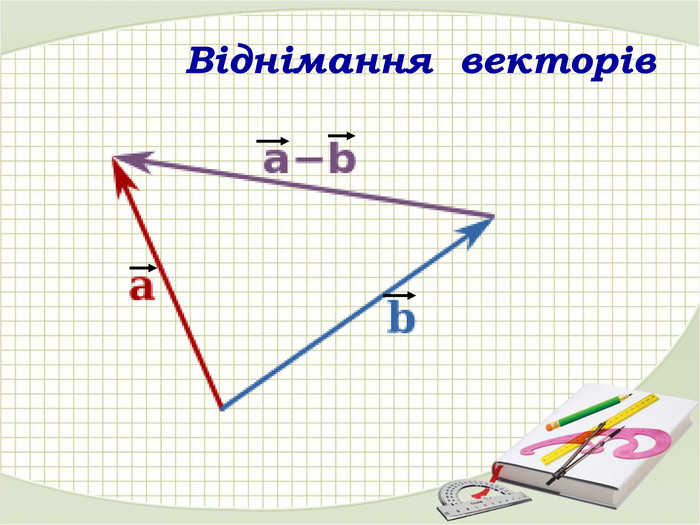
Віднімання векторів


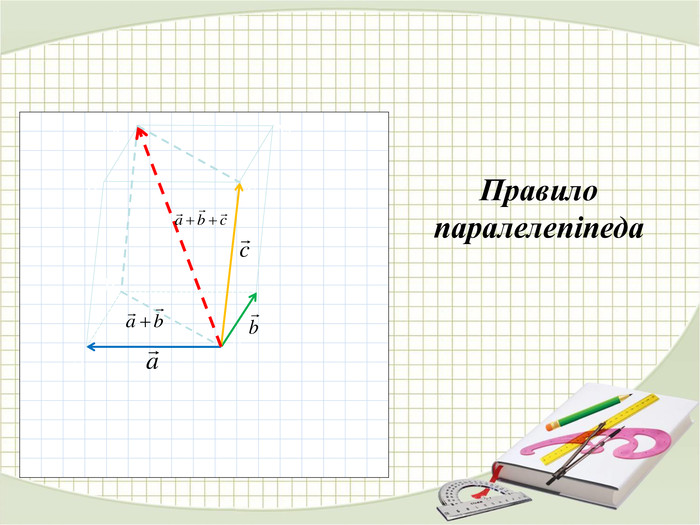
А О С М N D K B Правило паралелепіпеда


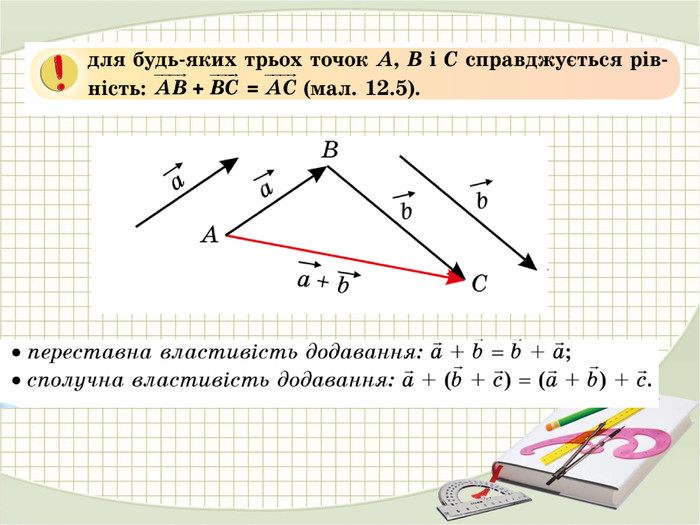
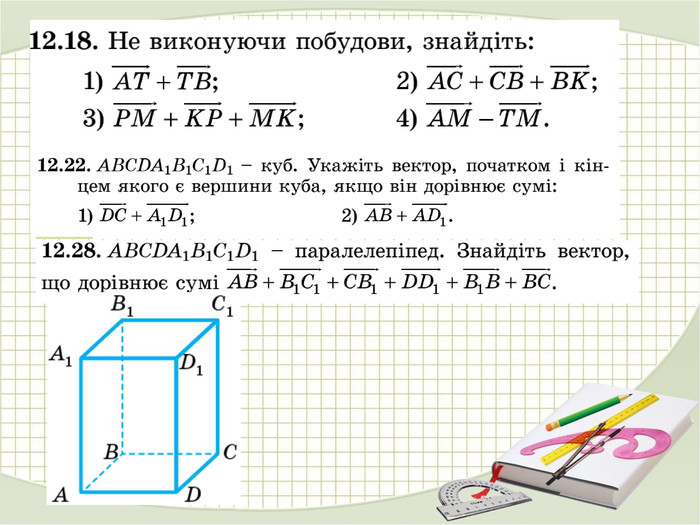
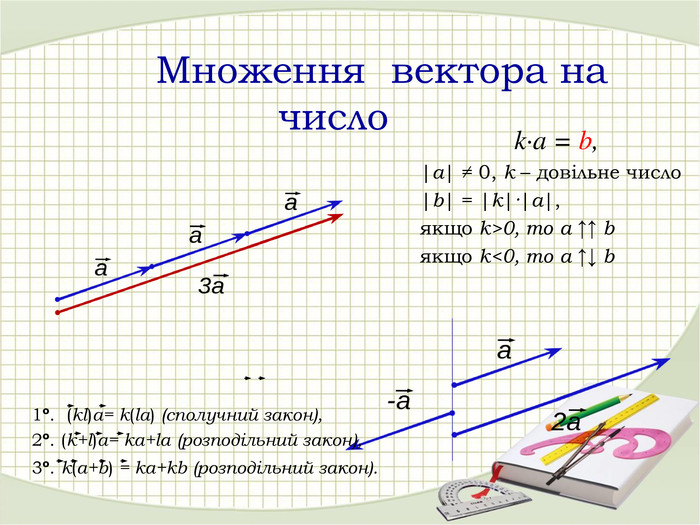
Множення вектора на число k·a = b, |a| ≠ 0, k – довільне число |b| = |k|·|a|, якщо k>0, то a ↑↑ b якщо k<0, то a ↑↓ b 1є. (kl)a= k(la) (сполучний закон), 2є. (k+l)a= ka+la (розподільний закон), 3є. k(a+b) = ka+kb (розподільний закон).


В зошитах записати основні поняття, формули.  ( таблиці)       

Картинки по запросу "вектори у просторі дії над векторами формули"
Картинки по запросу "вектори у просторі дії над векторами формули"



Учням  групи 204


Переглянути відео за посиланням   
https://www.youtube.com/watch?v=UdmG4JU2L4o


ТЕСТОВІ ЗАВДАННЯ

 З ТЕМИ «ВЕКТОРИ»








 Учням  групи   204. 
               Записати в робочий зошит тему  
               " Перетворення фігур в просторі. Cиметрія у просторі".  


      Поняття перетворення для фігур у просторі означають 
    так само, як і на   площині.
       Рухом називається перетворення, при якому зберігаються відстані 
                    між точками.
    Властивості руху в просторі:
    прямі переходять у прям, півпрямі  - у півпрямі, відрізки –
    у відрізки кути між  півпрямими зберігаються, площина переходить
    у площину.
      Зразки рухів у просторі:
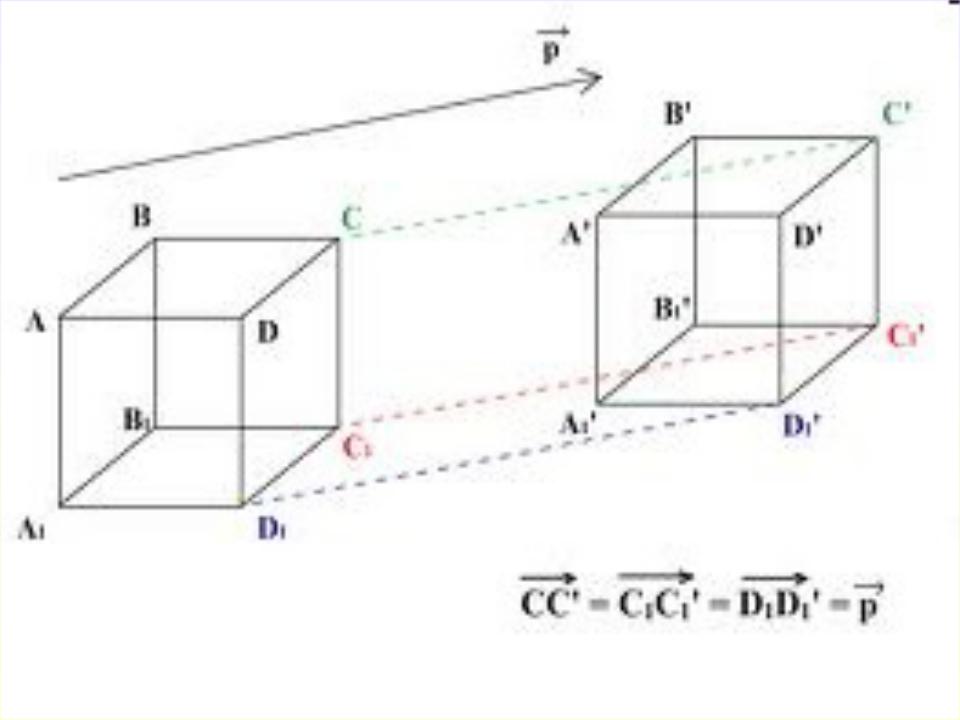
     1. Паралельним перенесенням у просторі називається  таке 
   перетворення, при  якому довільна точка (x; y; z) переходить у  
   точку (x+a; y+b; c+z), де числа  a, b, c– одні й ті самі для всіх точок 
                   (x; y; z).

        Паралельне перенесення є рухом.
        У результаті паралельного перенесення точки  зміщуються вздовж
                     паралельних прямих  (або прямих, що збігаються) на одну й ту 
                     саму відстань.
   1. У результаті паралельного перенесення кожна пряма 
   переходить у паралельну  їй пряму (або в себе).
   2.Які б не були точки А і А/ , існує єдине паралельне перенесення,  у 
   результаті  якого точка А переходить у точку А/ .
   3. У результаті паралельного перенесення в просторі
   кожна площина  переходить  або в себе, або в паралельну  їй площину.











движение симметрия и параллельный перенос - Стр 4













                     
         2. Подібність просторових фігур

    Перетворення фігури F називається перетворенням 
   подібності, якщо при цьому перетворенні відстані між точками 
   змінюють  себе в одну й ту саму кількість разів.
   Як і на площині, перетворення подібності в просторі переводить 
   прямі  у прямі, півпрямі у півпрямі, відрізки у відрізки і 
   зберігає кути між півпрямими. Перетворення подібності переводить 
   площини у площини.  
   Аналогічно гомотетії на площині визначається 
   г  омотетія в просторі.
   Гомотетія є перетворенням подібності.
   Перетворення гомотетії у просторі пере­водить довільну площину, 
   яка не проходить через центр гомотетії, у паралельну площину 
   (або в себе, якщо k = 1)

Презентація на тему «Гомотетія»

      3. Симетрія відносно точки; симетрія відносно прямої; симетрія 
      відносно площини (аналогічна симетрії відносно прямої).




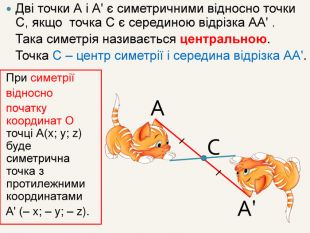
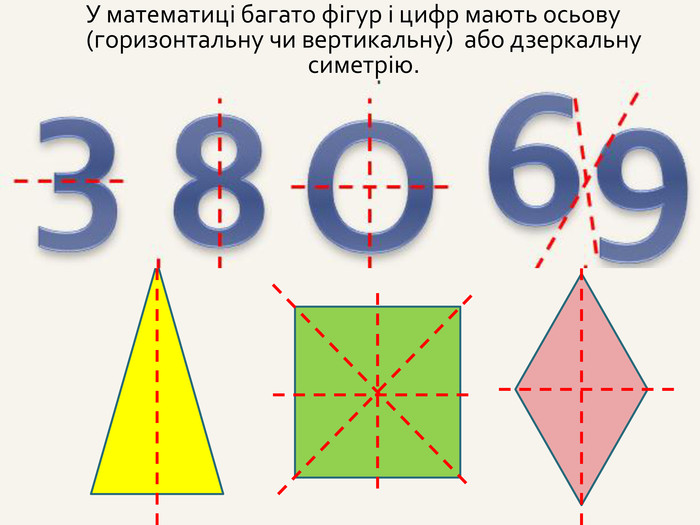
У математиці багато фігур і цифр мають осьову (горизонтальну чи вертикальну) або дзеркальну симетрію.

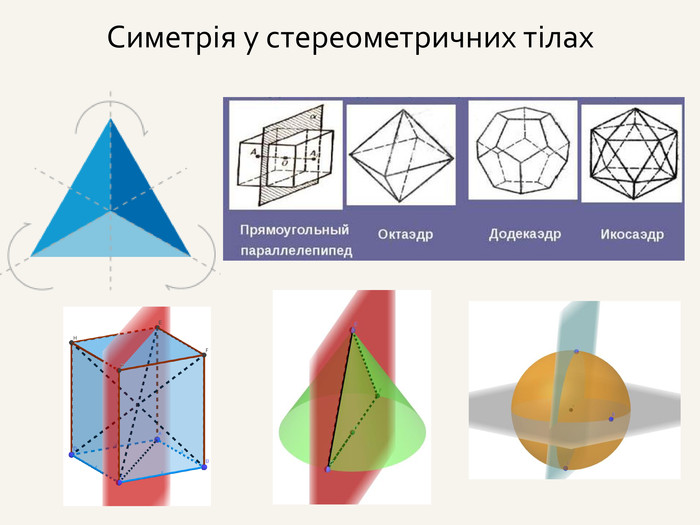
Симетрія у стереометричних тілах

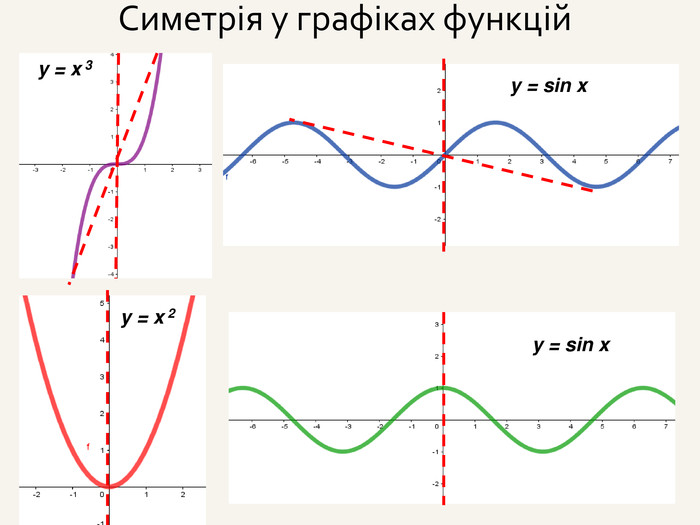
Симетрія у графіках функційy = sin x y = sin x y = x 3y = x 2

y = ǀ x ǀ

Симетрія у біології

У живій і неживій природі симетрія зустрічається дуже часто. Це зумовлено способом існування – несиметричні комахи і птахи не змогли б літати, листочки у рослинах затіняли б одне одного. Центральна і поворотна симетріїАденовірус. Медуза

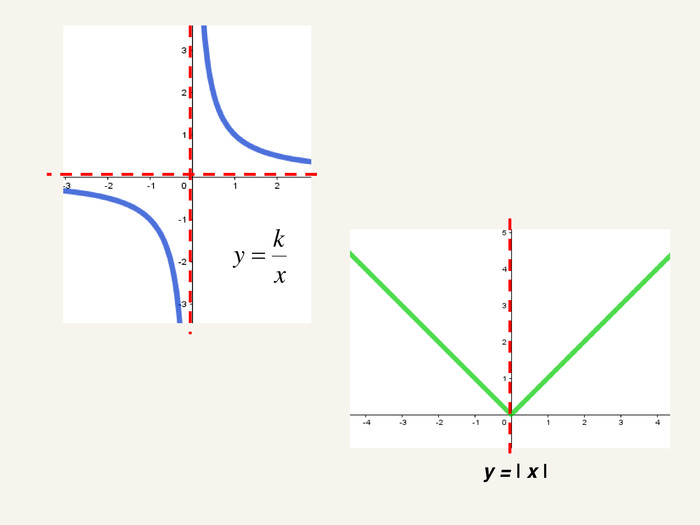
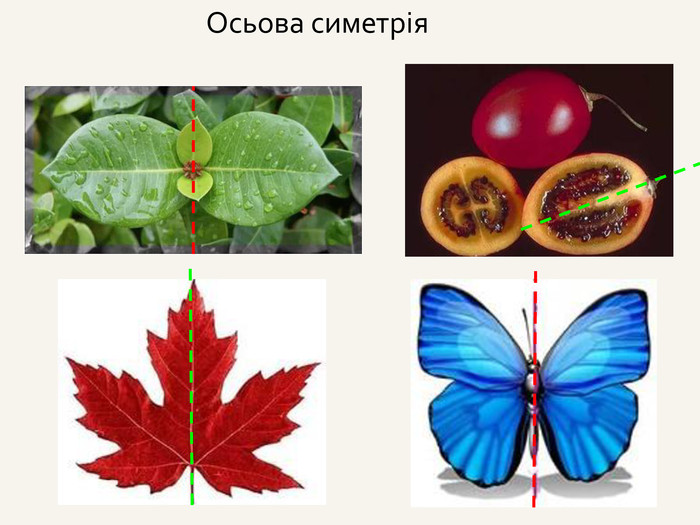
Осьова симетрія

Дзеркальна симетрія

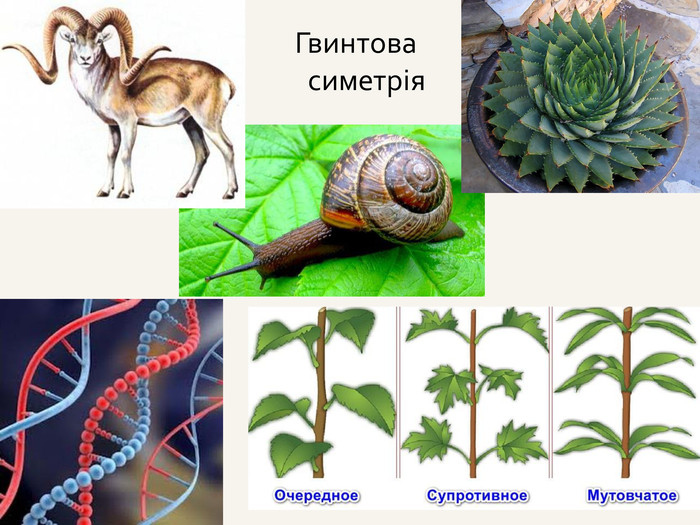
Гвинтова симетрія

Симетрія у фізиці і техніці

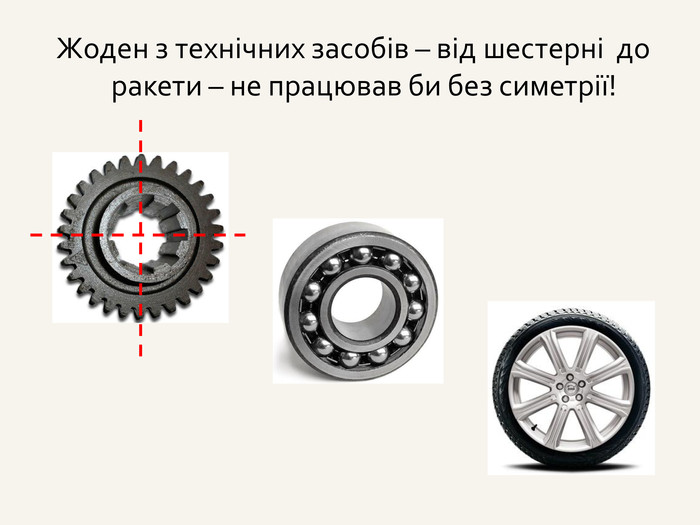
Жоден з технічних засобів – від шестерні до ракети – не працював би без симетрії!

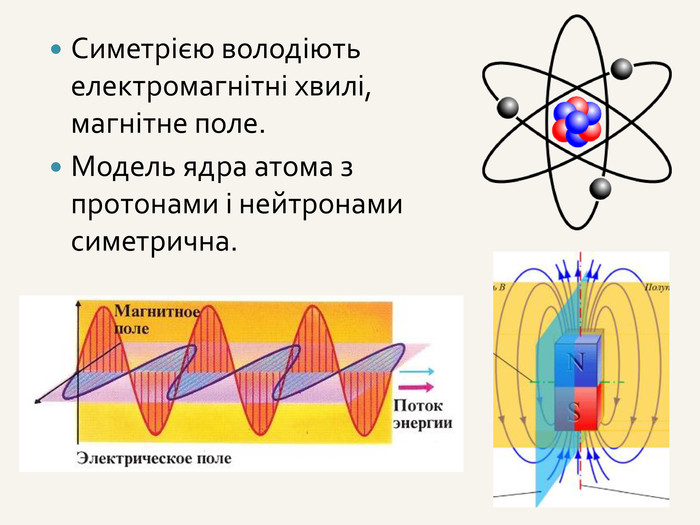
Симетрією володіють електромагнітні хвилі, магнітне поле. Модель ядра атома з протонами і нейтронами симетрична.

Симетрія в архітектурі

Вибираючи симетричні форми, архітектори прагнули досягти природної гармонії , як ознаки стійкості та рівноваги. Тадж-Махал, Індія. Собор Паризької БогоматеріПантеон
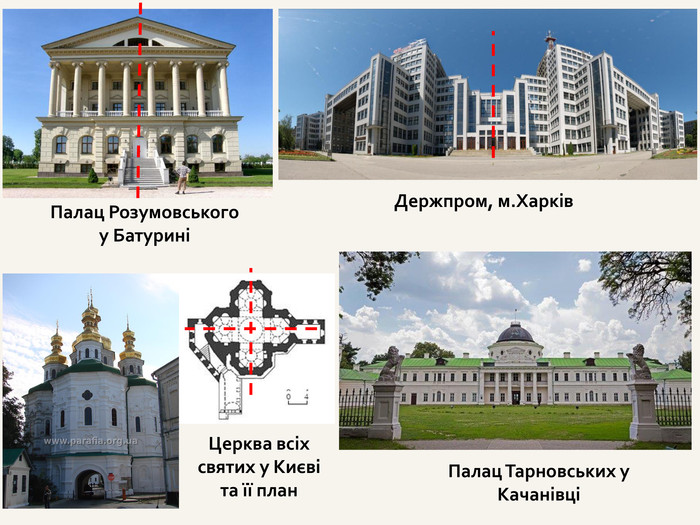
Церква всіх святих у Києві та її план. Палац Розумовського у БатуриніДержпром, м. Харків. Палац Тарновських у Качанівці

 Симетрія у мистецтві і побуті

Щодня у побуті ми стикаємося з проявами симетрії. Без симетрії не стояв би стілець, не трималися б окуляри, гвинт неможливо було б вкрутити.

Симетрія в українській вишивці

Симетрія в філології

Симетрія літер

Літературним праобразом амбіграм можна вважати паліндроми — слова або фрази, які читаються однаково як зліва направо, так і справа наліво.

Приклад
Дана точка .А (3; 5; 2)
Знайти точки, симетричні даній відносно координатних площин.
Відповідь: точка, симетрична точці А 
відносно Oху — це  (3; 5; -2); 
відносно Oyz — це    (-3; 5; 2); 
відносно Oxz — це   (3; -5; 2).

Розв’язати  самостійно:

    
    Для учнів 204 групи
     Урок: систематизація знань по темі "Координати і вектори у просторі.               Перетворення фігур у просторі", підготовка до тематичної контрольної             роботи.
      
    Вправа 1
        Читаємо запитання, якщо вірно ставимо знак (+),
якщо ні знак (-).

1. Чи правильно, що паралельне перенесення в просторі є переміщенням?
2. Чи правильно, що в результаті паралельного перенесення геометричне тіло може перейти само в себе?
3. Чи правильно, що два паралельних перенесення, виконаних послідовно, дають паралельне перенесення?
4. Чи правильно, що перетворення, обернене до паралельного перенесення, є тим же самим паралельним перенесенням?
5. Чи правильно, що в результаті паралельного перенесення площина переходить або в себе, або в паралельну площину?
6. Чи правильно, що для будь-яких точок А і В існує, і притому єдине, паралельне перенесення, у результаті якого точка  А  переходить  у точку В?
7. Чи існує переміщення, яке переводить одну із граней куба в іншу?
8. Якщо при гомотетії k=1, то отримаємо фігуру рівну даній?
9. Симетрія відносно площини є переміщенням?
10. Координати точки, симетричної точці А(1; 2; 3) відносно площини (ху)  дорівнюють (-1; 2; -3).
11. Координати точки, симетричної точці А(1; 2; 3) відносно осі 0у  дорівнюють (-1; 2; -3).
12. Координати точки, симетричної точці А(1; 2; 3) відносно початку координат  дорівнюють (-1; -2; -3).


Вправа 2
1.

2.

3.
    4.

    5. 

   
   6.

  7. 

  8. 

  9. 

   
   10.
    

 Для учнів 204 групи


Тематична контрольна робота
з теми "Координати і вектори у просторі".

 Перейти за посиланням
 https://naurok.com.ua/urok-kontrolna-robota-z-temi-koordinati-ta-vektori-v-prostori-33787.html

Виконуємо 1 варіант

 Для учнів 204 групи
                                         Підсумкова контрольна робота.
Початковий і середній рівень
1. Розв'яжіть нерівність:  0,6х  ≤  0,36.
А) (- ∞; 0,6);  Б) [0,6; + ∞);  В) (- ∞; 2];     Г) [2; + ∞).
2. Знайдіть значення виразу   log 5 250 – log5 2.
А)  3;     Б) 2;     В) 1;     Г) -3.
3. Коренем якого рівняння є число 16? 
А) log 8 x = 2;     Б) log 2 x = 8;     В) log 4 x = 2;     Г) log 4 x= 4.
4. Знайдіть похідну функції     f(x) = 4х3+ 6х.
А) 12х2;     Б) 12х2 + 6;    В) 4х2 + 6х;     Г) 4х4 + 6х2.
5. Знайдіть кутовий коефіцієнт дотичної, проведеної до графіка функції f (х) = х2 – 1 у точці з абсцисою х0 = 3.
А) 8;     Б) 7;     В) 6;     Г) 2.
6. Яка функція не має критичних точок?
А)  f (x) = x3;    Б) f (x) = x3 + 1;    В) f (x) = x3 + x;    Г) f (x) = x3 + x2.
7. Точка рухається по закону s(t) = 1 + 2t2 (м). Знайдіть швидкість руху точки в момент         часу t =1с.
А) 2 м/с;     Б) 4 м/с;    В) 3 м/с;     Г) 5 м/с.
8. Яка з точок лежить на осі абсцис?
А) (0; 3; - 1);     Б) (0; 0; 7);     В) (0; - 1; 0);     Г) (2; 0; 0).
9. Точка С - середина відрізка АВ,  А (2; 4; 6), С(0; 1; 10).
Знайдіть координати точки В.
А) В (1; 2,5; 8);     Б) В (-2; -2; 14);     В) В (-2; -3; 4);     Г) В (2; 6; 26).
10. Який вектор колінеарний вектору (- 4; 18; 6)?
А) (2; 9; - 3);     Б) (2; - 9; - 3);     В) (2; - 9; 3);     Г) (- 2; 9; - 3).
11. При  якому значенні n вектори  a ( 4; 2n - 1; - 1) і b ( 4; 9 - 3n; - 1) рівні?
А) - 2;     Б) 8;     В) 2;     Г) - 8.
12. Знайдіть координати вектора МК, якщо М(2; 4; - 3) і К(8; 1; 0).
А) (10; 5; - 3);     Б) (- 6; 3; - 3);     В) (6; - 3; 3);     Г) (16; 4; 0).
.
Достатній рівень
2.1. Знайдіть корінь рівняння:     9х+1 - 9х =24.
2.2.  Знайдіть проміжки зростання функції  f (x) = х3 – 3х2.
2.3. Знайдіть корені рівняння: log 2 x + log 2 (x - 3) = 2.
2.4. При якому значенні n вектори a(2; -1; n) і b(4; n; -5) перпендикулярні?
2.5. Розв’яжіть нерівніть  log 0,9 (x - 4) > log 0,9 (8 - x) .
Високий рівень
3.1. Розв’яжіть рівняння 2 ∙ 25х  - 5 ∙ 4х = 3 ∙ 10х
3.2 Розв’яжіть рівняння  log 6 (x - 2) + log 6 (x - 1) = 1.
3.3 Дано трикутник АВС. Знайдіть зовнішній кут при вершині С, якщо В(2;-1;-1), А(2;2;-4) і С(3;-1;-2).

Учням  групи 207 
 Записуємо в робочий зошит тему
« Багатогранники. Опуклі багатогранники». 

Переглянути відео за посиланням
https://www.youtube.com/watch?v=WvOauhM1TXQ

 В  зошитах записати

          Фігури, які вивчає стереометрія, називаються тілами. Наочно тіло уявляють як частину простору, зайняту фізичним тілом і обмежену поверхнею.

          Багатогранником називають тіло (частина простору), обмежене скінченою кількістю плоских многокутників.

           Багатокутники, які обмежують багатогранник, називають його гранями, їх сторони – ребрами, а вершини – вершинами багатогранника.    

             Багатогранник називається опуклим, якщо він лежить по один бік від площини кожного з плоских багатокутників на його поверхні. 

            Прикладами опуклих багатогранників можуть бути куб, прямокутний паралелепіпед, тетраедр тощо. 


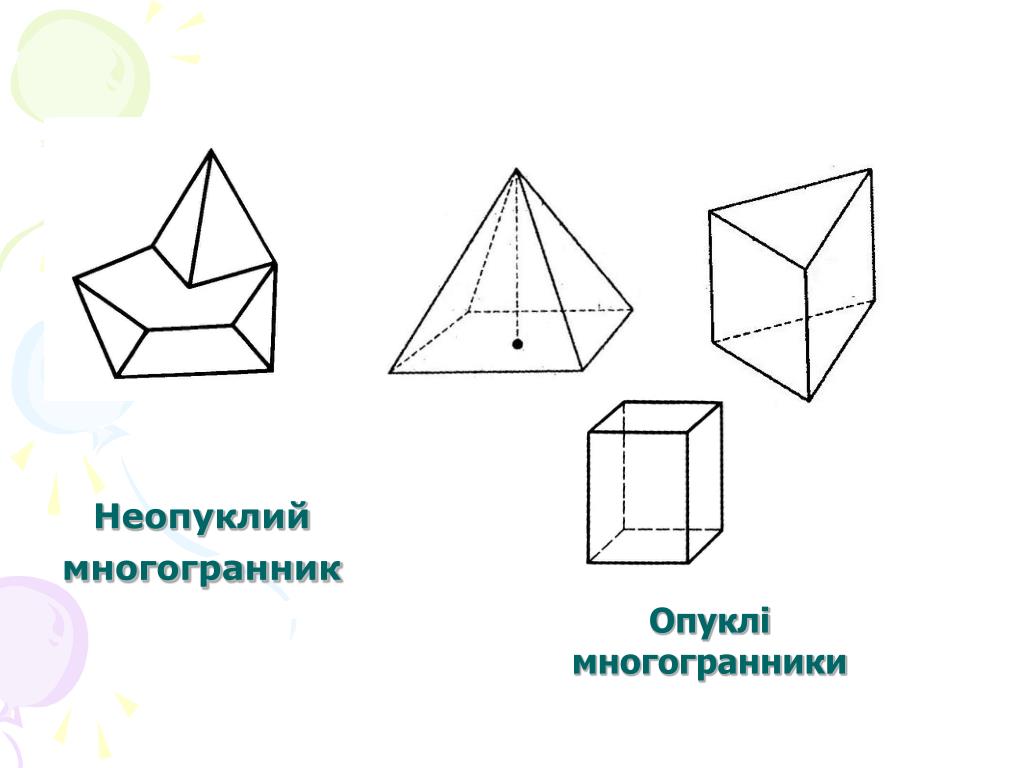
Картинки по запросу "Багатогранники. Опуклі багатогранники"
                  

      Дайте відповіді на питання:

 1. Наведіть приклади предметів побуту, що є геометричними тілами.
 2. Які із фігур, зображених на рисунку, є геометричними тілами?

а.                                                            б.
                














в.                                                                                      г.

                             




      




 3. Наведіть приклади предметів побуту, які мають форму багатогранника.
4. Наведіть приклади речовин, вивчених у курсі хімії, кристали яких мають форму багатогранника.
5. Скільки вершин, ребер, граней має: а) тетраедр;  б) куб?
6. Яке найменше число ребер може мати багатогранник? 
7. Побудуйте багатогранник, який має 4 грані. 
   Скільки ребер і скільки вершин він має? 
8. Скільки ребер може сходитися у вершині багатогранника?
9. Побудуйте багатогранник, у якого число вершин і число граней однакові.
10.Побудуйте багатогранник, який має 5 граней і 6 вершин. Скільки ребер він має? 

Учням  групи 207 

  Записуємо в робочий зошит тему
« Призма. Пряма і правильна призма. Паралелепіпед. Прямокутний паралелепіпед». 

 Конспект.
1.  Призма. Пряма і правильна призма.
 Призмою -  називається багатогранник, у якого дві грані — рівні n-кутники, розташовані в паралельних площинах, а решта n граней — паралелограми. 

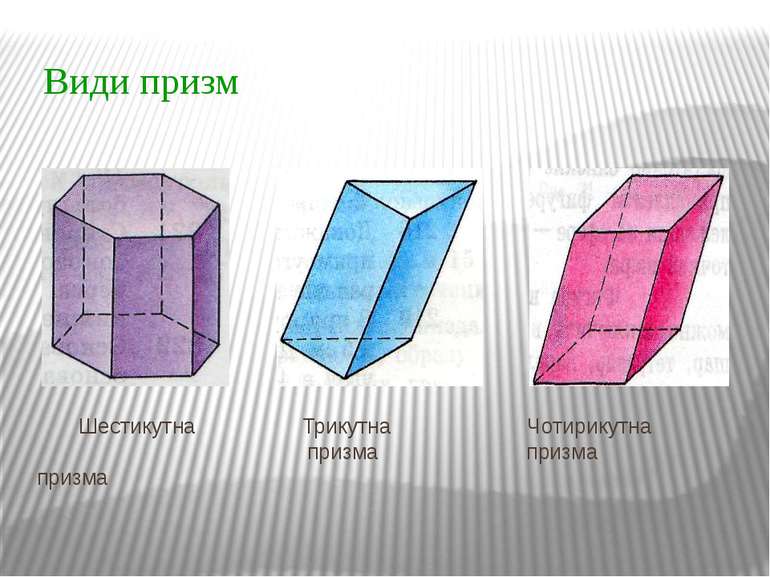
Картинки по запросу "Призма. Пряма і правильна призма."
          Властивості призми
•      Основи призми є рівними багатокутниками.
•      Бічні грані призми є паралелограмами.
•      Бічні ребра призми  рівні.
         Висота призми — відстань між площинами її основ.

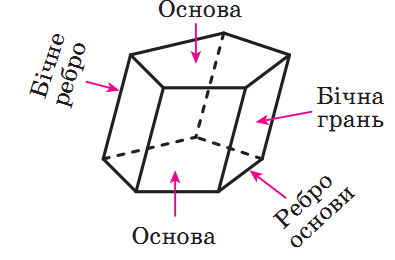
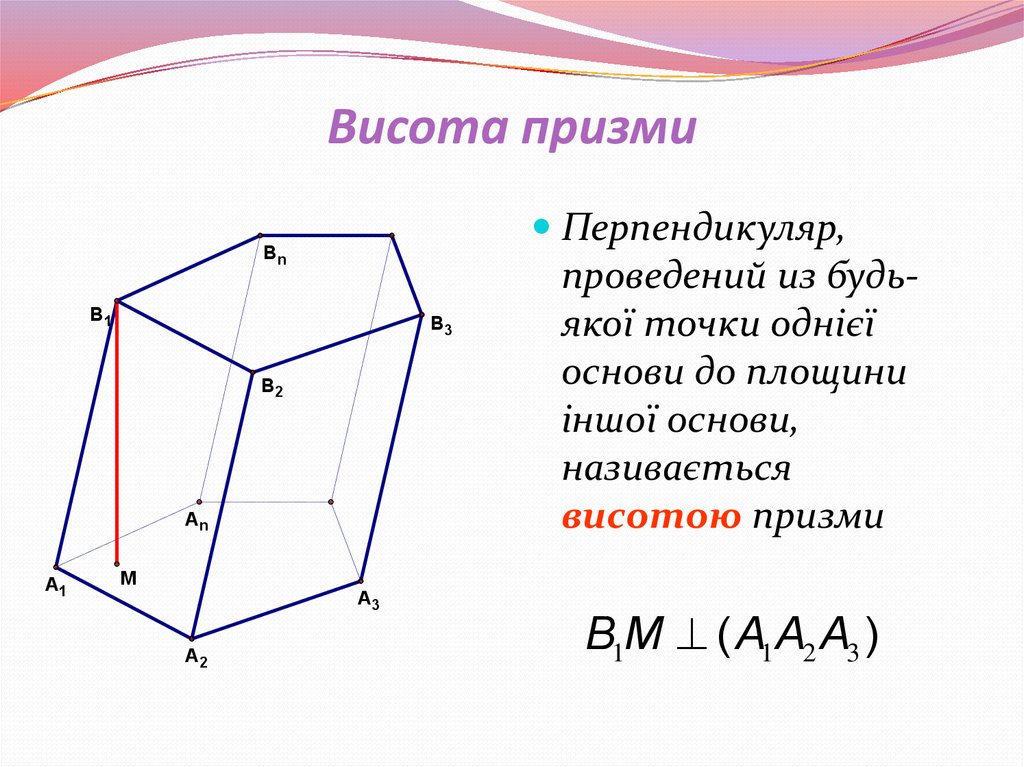
Картинки по запросу "Призма. Пряма і правильна призма."


Картинки по запросу "Призма. Пряма і правильна призма."

Картинки по запросу "Призма. Пряма і правильна призма."
Пряма призма – це призма, що має перпендикулярні до основ бічні ребра. Якщо ця умова не виконується, то призма називається похилою. 
У прямої призми всі бічні грані – прямокутники.


Картинки по запросу "ПРИЗМА Пряма і правильна призма"












      
Пряма призма, в основі якої лежить правильний багатокутник, називається правильною призмою.

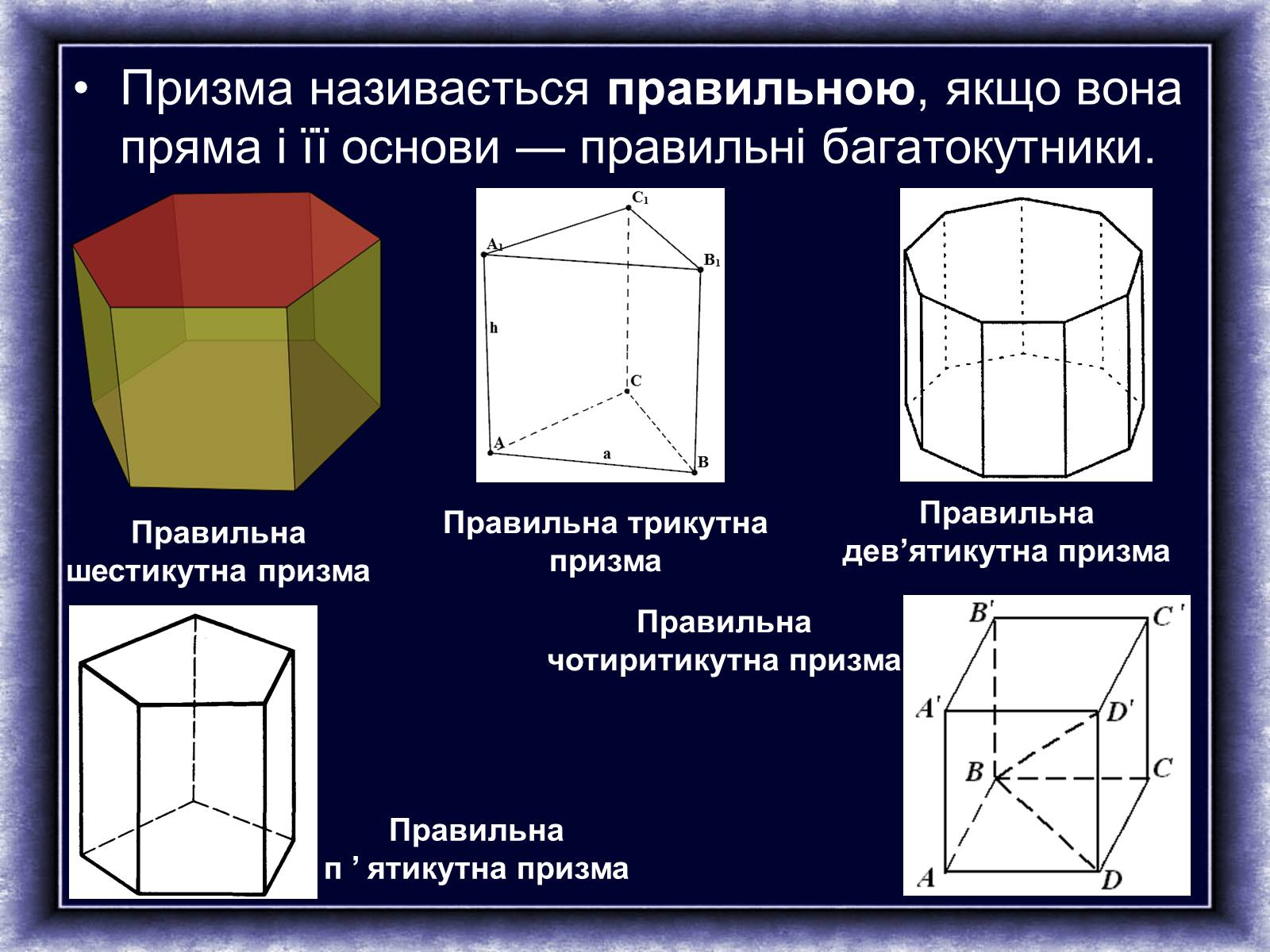
Картинки по запросу "Призма. Пряма і правильна призма."

 2. Паралелепіпед. Прямокутний паралелепіпед.
Паралелепіпед — це призма, основою якої є паралелограм.
Протилежні грані паралелепіпеда паралельні і рівні.
Діагоналі паралелепіпеда перетинаються в одній точці і діляться нею навпіл.

Картинки по запросу "Паралелепіпед ."

Прямий паралелепіпед  - це паралелепіпед, що має перпендикулярні до основ бічні ребра.
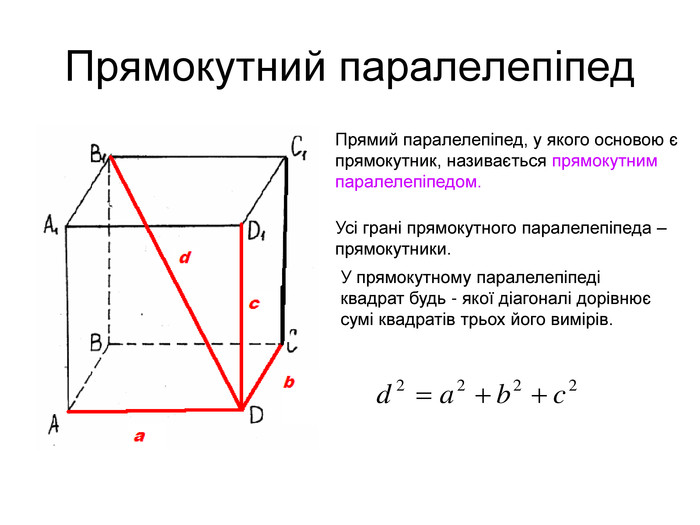
Прямокутний паралелепіпед — прямий паралелепіпед , основою якого є прямокутник.
Бічні грані прямокутного паралелепіпеда перпендикулярні його основам.
Лінійними розмірами прямокутного паралелепіпеда є довжини його непаралельних ребер. Прямокутний паралелепіпед, усі лінійні розміри якого рівні, називається кубом.
 

Картинки по запросу "Паралелепіпед ."

Діагоналі прямокутного паралелепіпеда рівні.
Усі двогранні кути прямокутного паралелепіпеда – прямі.
Квадрат будь-якої діагоналі прямокутного паралелепіпеда є сумою квадратів трьох його вимірів.
Точка перетину діагоналей паралелепіпеда є його центром симетрії.
Через центр симетрії прямокутного паралелепіпеда проходять три площини, паралельні граням, які є площинами симетрії прямокутного паралелепіпеда.
Картинки по запросу "Паралелепіпед ."
Завдання.


1.Яку форму має основа правильної чотирикутної призми:
А) правильний трикутник ;   Б)ромб ;    В) квадрат ;    г)прямокутник.

 2.Чому дорівнює висота прямої трикутної призми:

А)ребру основи ;       Б)бічному ребру ;    В) діагоналі ;    г) відразу визначити не можливо.

3.Скільки ребер має трикутна призма:

А) 3 ;   Б)6 ;    В) 9 ;     г) 10.?

4.У прямій шестикутній призмі діагональний переріз має форму:

А) правильного трикутника ;    Б)ромба ;    В) квадрата ;    г)прямокутника.

5.Висота правильної чотирикутної призми 8см, а діагональ основи 6 см. Чому дорівнює діагональ призми?
А) 8 см ;    Б)10см ;    В) 16см ;    г) 14см.

6.Всі ребра правильної трикутної призми дорівнюють по 3дм.Чому дорівнює площа       бічної поверхні призми?
А) 9дм2 ;    Б) 27дм2 ;   В) 36дм2 ;    г) 45дм2.

7.Віміри прямокутного паралелепіпеда дорівнюють 3см, 2см, 6 см. Знайдіть довжину діагоналі паралелепіпеда:

А) 8см ;    Б) 7см ;    В) 11см;   г) 3см.


 Учням  групи   207. 

Записати в робочий зошит тему  
"Піраміда. Правильна та зрізана піраміди". 

Переглянути презентацію по темі     "Піраміда".  



В робочий зошит  записати відповіді на питання:

1.  Який багатогранник називається пірамідою?
2.  Назвіть основні елементи піраміди.
3.  Яка піраміда називається правильною?
4. Властивості правильної піраміди.
5. Як знаходиться бічна поверхня правильної піраміди?
6. Яка піраміда називається зрізаною? 


Д/завдання
1. Сторона основи правильної чотирикутної піраміди 6см, висота 4см. 
Знайдіть повну поверхню піраміди.
2. Апофема правильної чотирикутної піраміди 5см, висота 3см. 
                      Знайдіть повну поверхню піраміди. 

     Учням  групи   207. 
       Записуємо в робочий зошит тему
     «Правильні багатогранники»

     Переглянути відео за посиланням




Завдання:
1. Знайдіть площу повної поверхні октаедра, якщо площа 
    однієї грані дорівнює  2 дм2.
2. Знайдіть площу повної поверхні куба, якщо площа 
    однієї грані  дорівнює   9 см2.
3. Знайдіть площу повної поверхні куба, якщо його 
    ребро дорівнює  2 см.   
4. Знайдіть площу повної поверхні правильного тетраедра, 
    ребро  якого  дорівнює 4 см.
5. Знайдіть діагональ куба, ребро якого дорівнює 1 дм.

        Учням  групи   207. 
  Урок:  Тематична контрольна робота з  теми:
”Багатогранники”

1.                          
         1.Сторона куба дорівнює 10 см. Знайти площу поверхні куба.
А
Б
В
Г
600 см²
400 см²
800 см²
360 см²

2.Знайдіть площу поверхні прямокутного паралелепіпеда, виміри якого               дорівнюють 2см, 3см і 4см.
А
Б
В
Г
24 см²
52 см²
18 см²
40 см²

3. Знайти діагональ прямокутного паралелепіпеда, виміри якого дорівнюють     2см, 3см і 6см.
А
Б
В
Г
5,5 см
36 см
11 см
7 см

4. Площа бічної грані правильної чотирикутної призми 48 см2, а периметр      основи – 12 см. Яке твердження правильне?
    
А
Б
В
Г
     Бічне ребро 4 см
Площа основи     призми 9 см2
     Площа діагонального перерізу 12 см2
     Всі грані призми - квадрати
5. Основою прямої призми є прямокутний трикутник з гіпотенузою 10см і катетом  6см. Знайти площу бічної поверхні призми, якщо її бічне ребро дорівнює 5см.
А
Б
В
Г
120 см²
90 см²
180 см²
60 см²

6. Величина двогранного кута при бічному ребрі правильної трикутної   призми дорівнює:
А
Б
В
Г
900
600
300
1200

7. В основі прямої призми лежить рівнобічна трапеція з основами 4см і 10см і бічною стороною 5см. Бічне ребро призми дорівнює 10см. Обчислити повну поверхню призми.
А
Б
В
Г
190 см²
296 см²
170 см²
186 см²

8. В основі прямої призми лежить прямокутник зі сторонами 6см і 8см.     Знайдіть бічну поверхню призми, якщо площа її діагонального перерізу дорівнює 40см².
А
Б
В
Г
88 см²
480 см²
112 см²
56 см²

9. Сторона основи правильної трикутної піраміди дорівнює 4см, апофема   6см. Знайти площу бічної поверхні піраміди. 
А
Б
В
Г
72 см²
24 см²
36 см²
48 см²

10.  Апофема правильної трикутної піраміди 6 см, плоский кут при вершині  900. Яке твердження є правильним?

А
Б
В
Г
    Бічна поверхня дорівнює
108 см2
Бічна поверхня дорівнює 54 см2
     Висота піраміди   2 см.

Площа основи дорівнює площі бічної грані

11. Апофема правильної трикутної піраміди дорівнює 6см, а радіус кола,   вписаного в її основу, дорівнює  см. Обчисліть бічну поверхню піраміди.

А
Б
В
Г
36 см2
54 см2
72 см2
інша відповідь

12. Основою піраміди є прямокутник зі сторонами 6см і 8 см. Знайти висоту   піраміди, якщо всі її бічні ребра рівні та дорівнюють 13см.
А
Б
В
Г
12 см
8 см
7 см
20см


Учням  групи   207. 
  Підсумкова контрольна робота.
Початковий і середній рівень
1. Розв'яжіть нерівність:  0,6х  ≤  0,36.
А) (- ∞; 0,6);  Б) [0,6; + ∞);  В) (- ∞; 2];     Г) [2; + ∞).
2. Знайдіть значення виразу   log 5 250 – log5 2.
А)  3;     Б) 2;     В) 1;     Г) -3.
3. Коренем якого рівняння є число 16? 
А) log 8 x = 2;   Б) log 2 x = 8;   В) log 4 x = 2;   Г) log 4 x= 4.
4. Знайдіть похідну функції f(x) = 4х3+ 6х.
А) 12х2;     Б) 12х2 + 6;    В) 4х2 + 6х;     Г) 4х4 + 6х2.
5. Знайдіть кутовий коефіцієнт дотичної, проведеної до                                      графіка функції f(х) = х2 – 1 у точці з абсцисою х0 = 3.
А) 8;     Б) 7;     В) 6;     Г) 2.
6. Яка функція не має критичних точок?
А)  f (x) = x3;   Б) f (x) = x3 + 1;                                                                            В) f (x) = x3 + x;   Г) f (x) = x3 + x2.
7. Точка рухається по закону s(t) = 1 + 2t2 (м). Знайдіть                                   швидкість руху точки в момент часу t =1с.

А) 2 м/с;     Б) 4 м/с;    В) 3 м/с;     Г) 5 м/с.

8. Який вектор колінеарний вектору (- 4; 18; 6)?
А) (2; 9; - 3);     Б) (2; - 9; - 3);     В) (2; - 9; 3);     Г) (- 2; 9; - 3).
9. Точка С - середина відрізка АВ,  А (2; 4; 6), С(0; 1; 10).
Знайдіть координати точки В.
А) В (1; 2,5; 8);     Б) В (-2; -2; 14);  
В) В (-2; -3; 4);     Г) В (2; 6; 26).
10. Обчисліть площу бічної поверхні прямої призми, основою якої є паралелограм зі сторонами 8 см і 22 см, а висота призми дорівнює 15см.
А) 900 см2;      Б) 450 см2;     В) 600 см2;     Г) 2640 см2.
11. При  якому значенні n вектори  a( 4; 2n - 1; - 1) і 
b( 4; 9 - 3n; - 1) рівні?
А) - 2;     Б) 8;     В) 2;     Г) - 8.
12. Знайдіть загальний вигляд первісних для функції  
f (x) = 5ex + 7sin x – 3x2.
 А) F(x) = 5ex – 7cos x – x3 ;   Б) F(x) = 5ex + 7cos x – x2 + C;   
 В) F(x) = 5ex – 7cos x – x3 + C;  Г) F(x) = ex+1 – 7 sin x – x3 .
Достатній рівень
2.1. Знайдіть корінь рівняння:     9х+1 - 9х =24.
2.2.  Знайдіть проміжки зростання функції  f (x)= х3 – 3х2.
2.3. Знайти площу фігури, обмеженої лініями  у = х3, х = 4,
 у = 0.
2.4. При якому значенні n вектори а(2; -1; n) і 
b(4; n; -5) перпендикулярні?
2.5.Основа прямої призми - ромб з діагоналями 10см і 24см. 
Менша діагональ призми дорівнює 26 см. Обчисліть площу 
бічної поверхні призми.
Високий рівень
11. Розв’яжіть рівняння log 6 (x - 2) + log 6 (x - 1) = 1.
12 Знайти площу фігури, обмеженої лініями  у = 1 – х  і  
у = 3 – 2х – х2.
13. . Основою піраміди є правильний трикутник. Одна з бічних граней піраміди перпендикулярна до площини основи, а дві інші нахилені до неї під кутом 600. Знайдіть об'єм піраміди, якщо її висота дорівнює  12см.


4 коментарі:

Підписатися на: Дописи (Atom)